| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 11 Perimeter and Area
Welcome to the comprehensive solutions guide for Chapter 11: Perimeter and Area. Building significantly upon the foundational concepts introduced in Class 6, this chapter delves deeper into the measurement of plane figures, commonly known as mensuration. While Class 6 focused primarily on the perimeter of rectilinear figures and the area of rectangles and squares, this chapter expands the repertoire considerably. It introduces systematic methods and formulas for calculating the area of crucial geometric shapes like parallelograms and triangles, and pioneers the exploration of circles, covering both their perimeter (circumference) and area. Mastering these concepts is essential not only for academic progress in mathematics and science but also for numerous practical applications in everyday life, from home improvement projects to understanding land measurements.
While the concept of perimeter – the total distance around a closed figure – is revisited, the predominant focus shifts towards understanding and calculating Area, the measure of the surface enclosed by a figure. The solutions provided offer detailed explanations and step-by-step applications of the new area formulas:
- Area of a Parallelogram: The solutions demonstrate that the area of a parallelogram is calculated using the formula: $\text{Area} = \text{base} \times \text{height}$. A critical point emphasized is that the 'height' ($h$) must be the perpendicular distance between the base ($b$) and the opposite side, not the length of the slanted side. Intuitive derivations, possibly involving transforming the parallelogram into a rectangle of equal area, might be illustrated.
- Area of a Triangle: The formula $\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$ (or $A = \frac{1}{2}bh$) is central here. Solutions often derive this by showing that a triangle is essentially half of a parallelogram sharing the same base and height. Again, the paramount importance of using the corresponding perpendicular height ($h$) relative to the chosen base ($b$) is stressed throughout the examples.
A significant advancement in this chapter is the introduction to the geometry of the Circle:
- Key terms are defined: Radius ($r$), Diameter ($d = 2r$), Circumference ($C$) – the perimeter or length of the boundary of the circle, and Area ($A$) – the space enclosed by the circle.
- The fundamental constant Pi ($\pi$) is introduced. Solutions explain that $\pi$ represents the constant ratio of a circle's circumference to its diameter ($\pi = \frac{C}{d}$). This irrational number is ubiquitous in circle calculations.
- The essential formulas are presented and applied:
- Circumference: $C = 2\pi r$ or $C = \pi d$.
- Area: $A = \pi r^2$.
- Solutions guide students through calculations using the commonly accepted approximate values for Pi: $\pi \approx \frac{22}{7}$ or $\pi \approx 3.14$. Problems involve finding the circumference or area given the radius/diameter, and conversely, determining the radius or diameter if the circumference or area is known (requiring algebraic manipulation like finding $r = \sqrt{\frac{A}{\pi}}$).
A crucial aspect emphasized in the solutions is the application of these formulas to solve practical, multi-step word problems. Examples include:
- Calculating the area of pathways constructed either around or inside rectangular or circular fields/parks (often involving subtracting the area of the inner shape from the area of the outer shape).
- Determining costs associated with area, such as the cost of tiling a floor, leveling a ground, or painting a wall, typically calculated as $\text{Total Cost} = \text{Area} \times \text{Rate per unit area}$ (e.g., rate in $\textsf{₹}$ per $m^2$).
- Finding the number of revolutions a circular wheel makes to cover a specific distance, linking distance to circumference ($\text{Distance} = \text{Number of revolutions} \times \text{Circumference}$).
- Comparing the areas of different geometric shapes.
Additionally, the importance of maintaining consistent units and performing necessary unit conversions (e.g., converting $cm^2$ to $m^2$, or understanding units like hectares where $1 \text{ hectare} = 10000 \text{ } m^2$) is addressed within the problem-solving process. These detailed solutions aim to build both computational proficiency and strong problem-solving skills in mensuration.
Example 1 to 5 (Before Exercise 11.1)
Example 1. A door-frame of dimensions 3 m × 2 m is fixed on the wall of dimension 10 m × 10 m. Find the total labour charges for painting the wall if the labour charges for painting 1 m2 of the wall is ₹ 2.50.
Answer:
Given:
Dimensions of the wall = 10 m × 10 m
Dimensions of the door-frame = 3 m × 2 m
Labour charges for painting 1 m2 of the wall =
To Find:
The total labour charges for painting the wall.
Solution:
First, we need to find the area of the wall that needs to be painted. This is the total area of the wall minus the area of the door-frame, as the door-frame will not be painted.
Area of the wall = Length × Breadth
$= 10 \text{ m} \times 10 \text{ m}$
$= 100 \text{ m}^2$
Area of the door-frame = Length × Breadth
$= 3 \text{ m} \times 2 \text{ m}$
$= 6 \text{ m}^2$
Now, the area of the wall to be painted = Area of the wall - Area of the door-frame
$= 100 \text{ m}^2 - 6 \text{ m}^2$
$= 94 \text{ m}^2$
The labour charges for painting 1 m2 is
Therefore, the total labour charges for painting 94 m2 of the wall is:
$= \text{Area to be painted} \times \text{Rate per m}^2$
$= 94 \times \textsf{₹} 2.50$
$= \textsf{₹} 235.00$
Hence, the total labour charges for painting the wall is
Example 2. The area of a rectangular sheet is 500 cm2 . If the length of the sheet is 25 cm, what is its width? Also find the perimeter of the rectangular sheet.
Answer:
Given:
Area of the rectangular sheet = 500 cm2
Length of the rectangular sheet (l) = 25 cm
To Find:
1. Width of the rectangular sheet (b)
2. Perimeter of the rectangular sheet
Solution:
We know the formula for the area of a rectangle:
$Area \ = \ length \ \times \ width$
$A \ = \ l \ \times \ b$
Substitute the given values:
$500 \ cm^2 \ = \ 25 \ cm \ \times \ b$
To find the width (b), we rearrange the formula:
$b \ = \ \frac{Area}{length}$
$b \ = \ \frac{500 \ cm^2}{25 \ cm}$
$b \ = \ 20 \ cm$
So, the width of the rectangular sheet is 20 cm.
Now, we find the perimeter of the rectangular sheet using the formula:
$Perimeter \ = \ 2 \ \times \ (length \ + \ width)$
$P \ = \ 2(l \ + \ b)$
Substitute the values of length and the calculated width:
$P \ = \ 2(25 \ cm \ + \ 20 \ cm)$
$P \ = \ 2(45 \ cm)$
$P \ = \ 90 \ cm$
So, the perimeter of the rectangular sheet is 90 cm.
Final Answer:
The width of the rectangular sheet is 20 cm and its perimeter is 90 cm.
Example 3. Anu wants to fence the garden in front of her house (Fig 11.5), on three sides with lengths 20 m, 12 m and 12 m. Find the cost of fencing at the rate of ₹ 150 per metre.

Answer:
Given:
Shape of the garden is rectangular (as inferred from the diagram and typical house-adjacent gardens).
The fencing is required only on three sides.
Lengths of the three sides to be fenced = 20 m, 12 m, and 12 m.
Rate of fencing =
To Find:
The total cost of fencing the garden on three sides.
Solution:
First, we need to find the total length of the fence required. Since the garden is fenced on three sides, the length required is the sum of the lengths of these three sides.
Total length of fence = Length of side 1 + Length of side 2 + Length of side 3
Total length of fence = $20 \ m \ + \ 12 \ m \ + \ 12 \ m$
Total length of fence = $44 \ m$
Next, we calculate the total cost of fencing.
Total cost = Total length of fence $\times$ Rate per metre
Total cost = $44 \ m \ \times \ \textsf{₹} 150 m$
Total cost =
Final Answer:
The total cost of fencing the garden on three sides is
Example 4. A wire is in the shape of a square of side 10 cm. If the wire is rebent into a rectangle of length 12 cm, find its breadth. Which encloses more area, the square or the rectangle?
Answer:
Given:
1. A wire is initially in the shape of a square.
Side of the square (s) = 10 cm
2. The same wire is rebent into the shape of a rectangle.
Length of the rectangle (l) = 12 cm
To Find:
1. Breadth of the rectangle (b)
2. Which shape (square or rectangle) encloses more area?
Solution:
Step 1: Find the length of the wire
The length of the wire is equal to the perimeter of the square.
Perimeter of the square = $4 \ \times \ side \ = \ 4 \ \times \ s$
Perimeter of the square = $4 \ \times \ 10 \ cm \ = \ 40 \ cm$
So, the total length of the wire is 40 cm.
Step 2: Find the breadth of the rectangle
When the wire is rebent into a rectangle, its length remains the same. Therefore, the perimeter of the rectangle is equal to the length of the wire (which is the perimeter of the square).
Perimeter of the rectangle = 40 cm
We know the formula for the perimeter of a rectangle:
Perimeter = $2 \ \times \ (length \ + \ breadth) \ = \ 2(l \ + \ b)$
Substitute the known values:
$40 \ cm \ = \ 2 \ \times \ (12 \ cm \ + \ b)$
Divide both sides by 2:
$\frac{40}{2} \ = \ 12 \ + \ b$
$20 \ = \ 12 \ + \ b$
Subtract 12 from both sides to find b:
$b \ = \ 20 \ - \ 12$
$b \ = \ 8 \ cm$
The breadth of the rectangle is 8 cm.
Step 3: Compare the areas
Calculate the area of the square:
Area of square = $side \ \times \ side \ = \ s^2$
Area of square = $(10 \ cm)^2 \ = \ 10 \ cm \ \times \ 10 \ cm \ = \ 100 \ cm^2$
Calculate the area of the rectangle:
Area of rectangle = $length \ \times \ breadth \ = \ l \ \times \ b$
Area of rectangle = $12 \ cm \ \times \ 8 \ cm \ = \ 96 \ cm^2$
Compare the areas:
Area of square = 100 cm2
Area of rectangle = 96 cm2
Since $100 \ cm^2 \ > \ 96 \ cm^2$, the square encloses more area than the rectangle.
Final Answer:
The breadth of the rectangle is 8 cm.
The square encloses more area than the rectangle.
Example 5. The area of a square and a rectangle are equal. If the side of the square is 40 cm and the breadth of the rectangle is 25 cm, find the length of the rectangle. Also, find the perimeter of the rectangle.
Answer:
Given:
1. Area of a square is equal to the area of a rectangle.
2. Side of the square (s) = 40 cm.
3. Breadth of the rectangle (b) = 25 cm.
To Find:
1. Length of the rectangle (l).
2. Perimeter of the rectangle.
Solution:
Step 1: Calculate the area of the square
Area of square = $side \ \times \ side \ = \ s^2$
Area of square = $(40 \ cm)^2 \ = \ 40 \ cm \ \times \ 40 \ cm \ = \ 1600 \ cm^2$
Step 2: Find the length of the rectangle
We are given that the area of the rectangle is equal to the area of the square.
Area of rectangle = Area of square = 1600 cm2.
We know the formula for the area of a rectangle:
$Area \ = \ length \ \times \ breadth$
$A \ = \ l \ \times \ b$
Substitute the known values for the rectangle:
$1600 \ cm^2 \ = \ l \ \times \ 25 \ cm$
To find the length (l), rearrange the formula:
$l \ = \ \frac{Area}{breadth}$
$l \ = \ \frac{1600 \ cm^2}{25 \ cm}$
Calculation: $1600 \ \div \ 25 \ = \ 64$
$l \ = \ 64 \ cm$
The length of the rectangle is 64 cm.
Step 3: Find the perimeter of the rectangle
Now we use the formula for the perimeter of a rectangle:
$Perimeter \ = \ 2 \ \times \ (length \ + \ breadth)$
$P \ = \ 2(l \ + \ b)$
Substitute the values of the length and breadth of the rectangle:
$P \ = \ 2(64 \ cm \ + \ 25 \ cm)$
$P \ = \ 2(89 \ cm)$
$P \ = \ 178 \ cm$
The perimeter of the rectangle is 178 cm.
Final Answer:
The length of the rectangle is 64 cm and its perimeter is 178 cm.
Exercise 11.1
Question 1. The length and the breadth of a rectangular piece of land are 500 m and 300 m respectively. Find
(i) its area
(ii) the cost of the land, if 1 m2 of the land costs ₹ 10,000.
Answer:
Given:
Length of the rectangular piece of land (l) = 500 m
Breadth of the rectangular piece of land (b) = 300 m
Cost rate of the land =
To Find:
(i) Area of the land
(ii) Total cost of the land
Solution:
(i) Finding the area of the land
We use the formula for the area of a rectangle:
$Area \ = \ length \ \times \ breadth$
$A \ = \ l \ \times \ b$
Substitute the given values:
$A \ = \ 500 \ m \ \times \ 300 \ m$
$A \ = \ 1,50,000 \ m^2$
The area of the rectangular piece of land is 1,50,000 m2.
(ii) Finding the cost of the land
The cost is calculated by multiplying the total area by the cost per square metre.
Total Cost = Area $\times$ Cost per m2
Total Cost = $1,50,000 \ m^2 \ \times \ \textsf{₹} 10,000 / m^2$
Total Cost =
Total Cost =
The total cost of the land is
Final Answer:
(i) The area of the land is 1,50,000 m2.
(ii) The cost of the land is
Question 2. Find the area of a square park whose perimeter is 320 m.
Answer:
Given:
Shape of the park is a square.
Perimeter of the square park = 320 m.
To Find:
Area of the square park.
Solution:
Step 1: Find the side length of the square park
Let the side length of the square park be 's'.
The formula for the perimeter of a square is:
$Perimeter \ = \ 4 \ \times \ side$
$P \ = \ 4s$
Substitute the given perimeter:
$320 \ m \ = \ 4s$
To find the side length (s), divide the perimeter by 4:
$s \ = \ \frac{320 \ m}{4}$
$s \ = \ 80 \ m$
The side length of the square park is 80 m.
Step 2: Find the area of the square park
The formula for the area of a square is:
$Area \ = \ side \ \times \ side$
$A \ = \ s^2$
Substitute the calculated side length:
$A \ = \ (80 \ m)^2$
$A \ = \ 80 \ m \ \times \ 80 \ m$
$A \ = \ 6400 \ m^2$
The area of the square park is 6400 m2.
Final Answer:
The area of the square park is 6400 m2.
Question 3. Find the breadth of a rectangular plot of land, if its area is 440 m2 and the length is 22 m. Also find its perimeter.
Answer:
Given:
Shape of the plot of land is rectangular.
Area of the rectangular plot (A) = 440 m2
Length of the rectangular plot (l) = 22 m
To Find:
1. Breadth of the rectangular plot (b)
2. Perimeter of the rectangular plot (P)
Solution:
Step 1: Find the breadth of the rectangular plot
We use the formula for the area of a rectangle:
$Area \ = \ length \ \times \ breadth$
$A \ = \ l \ \times \ b$
Substitute the given values:
$440 \ m^2 \ = \ 22 \ m \ \times \ b$
To find the breadth (b), rearrange the formula:
$b \ = \ \frac{Area}{length}$
$b \ = \ \frac{440 \ m^2}{22 \ m}$
$b \ = \ 20 \ m$
The breadth of the rectangular plot is 20 m.
Step 2: Find the perimeter of the rectangular plot
Now we use the formula for the perimeter of a rectangle:
$Perimeter \ = \ 2 \ \times \ (length \ + \ breadth)$
$P \ = \ 2(l \ + \ b)$
Substitute the values of the length and the calculated breadth:
$P \ = \ 2(22 \ m \ + \ 20 \ m)$
$P \ = \ 2(42 \ m)$
$P \ = \ 84 \ m$
The perimeter of the rectangular plot is 84 m.
Final Answer:
The breadth of the rectangular plot is 20 m and its perimeter is 84 m.
Question 4. The perimeter of a rectangular sheet is 100 cm. If the length is 35 cm, find its breadth. Also find the area.
Answer:
Given:
Perimeter of the rectangular sheet (P) = 100 cm
Length of the rectangular sheet (l) = 35 cm
To Find:
1. Breadth of the rectangular sheet (b)
2. Area of the rectangular sheet (A)
Solution:
Step 1: Find the breadth of the rectangular sheet
We use the formula for the perimeter of a rectangle:
$Perimeter \ = \ 2 \ \times \ (length \ + \ breadth)$
$P \ = \ 2(l \ + \ b)$
Substitute the given values:
$100 \ cm \ = \ 2(35 \ cm \ + \ b)$
Divide both sides of the equation by 2:
$\frac{100}{2} \ = \ 35 \ + \ b$
$50 \ = \ 35 \ + \ b$
To find the breadth (b), subtract 35 from both sides:
$b \ = \ 50 \ - \ 35$
$b \ = \ 15 \ cm$
The breadth of the rectangular sheet is 15 cm.
Step 2: Find the area of the rectangular sheet
Now we use the formula for the area of a rectangle:
$Area \ = \ length \ \times \ breadth$
$A \ = \ l \ \times \ b$
Substitute the values of the length and the calculated breadth:
$A \ = \ 35 \ cm \ \times \ 15 \ cm$
$A \ = \ 525 \ cm^2$
The area of the rectangular sheet is 525 cm2.
Final Answer:
The breadth of the rectangular sheet is 15 cm and its area is 525 cm2.
Question 5. The area of a square park is the same as of a rectangular park. If the side of the square park is 60 m and the length of the rectangular park is 90 m, find the breadth of the rectangular park.
Answer:
Given:
1. Area of a square park = Area of a rectangular park.
2. Side of the square park (s) = 60 m.
3. Length of the rectangular park (l) = 90 m.
To Find:
Breadth of the rectangular park (b).
Solution:
Step 1: Calculate the area of the square park
Area of square = $side \ \times \ side \ = \ s^2$
Area of square = $(60 \ m)^2 \ = \ 60 \ m \ \times \ 60 \ m \ = \ 3600 \ m^2$
Step 2: Find the breadth of the rectangular park
We are given that the area of the rectangular park is equal to the area of the square park.
Area of rectangular park = Area of square park = 3600 m2.
We know the formula for the area of a rectangle:
$Area \ = \ length \ \times \ breadth$
$A \ = \ l \ \times \ b$
Substitute the known values for the rectangle:
$3600 \ m^2 \ = \ 90 \ m \ \times \ b$
To find the breadth (b), rearrange the formula:
$b \ = \ \frac{Area}{length}$
$b \ = \ \frac{3600 \ m^2}{90 \ m}$
$b \ = \ \frac{360}{9} \ m$
$b \ = \ 40 \ m$
The breadth of the rectangular park is 40 m.
Final Answer:
The breadth of the rectangular park is 40 m.
Question 6. A wire is in the shape of a rectangle. Its length is 40 cm and breadth is 22 cm. If the same wire is rebent in the shape of a square, what will be the measure of each side. Also find which shape encloses more area?
Answer:
Given:
1. Initial shape of the wire: Rectangle.
Length of the rectangle (l) = 40 cm.
Breadth of the rectangle (b) = 22 cm.
2. Final shape of the wire: Square.
3. The total length of the wire remains the same.
To Find:
1. Measure of each side of the square (s).
2. Which shape (rectangle or square) encloses more area?
Solution:
Step 1: Find the length of the wire (Perimeter of the rectangle)
The length of the wire is equal to the perimeter of the initial rectangular shape.
Perimeter of rectangle = $2 \ \times \ (length \ + \ breadth)$
$P_{rect} \ = \ 2(l \ + \ b)$
Substitute the given values:
$P_{rect} \ = \ 2(40 \ cm \ + \ 22 \ cm)$
$P_{rect} \ = \ 2(62 \ cm)$
$P_{rect} \ = \ 124 \ cm$
So, the total length of the wire is 124 cm.
Step 2: Find the side of the square
When the wire is rebent into a square, its perimeter remains the same as the length of the wire.
Perimeter of the square ($P_{square}$) = 124 cm.
Let the side of the square be 's'.
The formula for the perimeter of a square is:
$P_{square} \ = \ 4 \ \times \ side \ = \ 4s$
Substitute the perimeter:
$124 \ cm \ = \ 4s$
To find the side (s), divide the perimeter by 4:
$s \ = \ \frac{124 \ cm}{4}$
$s \ = \ 31 \ cm$
The measure of each side of the square is 31 cm.
Step 3: Compare the areas
Calculate the area of the original rectangle:
$Area_{rect} \ = \ length \ \times \ breadth \ = \ l \ \times \ b$
$Area_{rect} \ = \ 40 \ cm \ \times \ 22 \ cm$
$Area_{rect} \ = \ 880 \ cm^2$
Calculate the area of the square:
$Area_{square} \ = \ side \ \times \ side \ = \ s^2$
$Area_{square} \ = \ (31 \ cm)^2 \ = \ 31 \ cm \ \times \ 31 \ cm$
$Area_{square} \ = \ 961 \ cm^2$
Compare the areas:
Area of square = 961 cm2
Area of rectangle = 880 cm2
Since $961 \ cm^2 \ > \ 880 \ cm^2$, the square encloses more area than the rectangle.
Final Answer:
The measure of each side of the square is 31 cm.
The square shape encloses more area.
Question 7. The perimeter of a rectangle is 130 cm. If the breadth of the rectangle is 30 cm, find its length. Also find the area of the rectangle.
Answer:
Given:
Perimeter of the rectangle (P) = 130 cm
Breadth of the rectangle (b) = 30 cm
To Find:
1. Length of the rectangle (l)
2. Area of the rectangle (A)
Solution:
Step 1: Find the length of the rectangle
We use the formula for the perimeter of a rectangle:
$P \ = \ 2(l \ + \ b)$
Substitute the given values:
$130 \ cm \ = \ 2(l \ + \ 30 \ cm)$
Divide both sides of the equation by 2:
$\frac{130}{2} \ = \ l \ + \ 30$
$65 \ = \ l \ + \ 30$
To find the length (l), subtract 30 from both sides:
$l \ = \ 65 \ - \ 30$
$l \ = \ 35 \ cm$
The length of the rectangle is 35 cm.
Step 2: Find the area of the rectangle
Now we use the formula for the area of a rectangle:
$Area \ = \ length \ \times \ breadth$
$A \ = \ l \ \times \ b$
Substitute the values of the calculated length and the given breadth:
$A \ = \ 35 \ cm \ \times \ 30 \ cm$
$A \ = \ 1050 \ cm^2$
The area of the rectangle is 1050 cm2.
Final Answer:
The length of the rectangle is 35 cm and its area is 1050 cm2.
Question 8. A door of length 2 m and breadth 1m is fitted in a wall. The length of the wall is 4.5 m and the breadth is 3.6 m (Fig11.6). Find the cost of white washing the wall, if the rate of white washing the wall is ₹ 20 per m2.
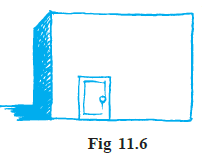
Answer:
Given:
Length of the door = 2 m
Breadth of the door = 1 m
Length of the wall = 4.5 m
Breadth of the wall = 3.6 m
Rate of white washing the wall =
To Find:
The cost of white washing the wall.
Solution:
First, we need to find the area of the wall that needs to be white washed. This area is the total area of the wall excluding the area of the door.
Area of the rectangular wall = Length × Breadth
$= 4.5 \text{ m} \times 3.6 \text{ m}$
$= 16.2 \text{ m}^2$
Area of the door = Length × Breadth
$= 2 \text{ m} \times 1 \text{ m}$
$= 2 \text{ m}^2$
Now, the area of the wall to be white washed = Area of the wall - Area of the door
$= 16.2 \text{ m}^2 - 2 \text{ m}^2$
$= 14.2 \text{ m}^2$
The rate of white washing is
Therefore, the total cost of white washing the wall is:
$= \text{Area to be white washed} \times \text{Rate per m}^2$
$= 14.2 \times \textsf{₹} 20$
$= \textsf{₹} 284$
Hence, the cost of white washing the wall is
Example 6 to 11 (Before Exercise 11.2)
Example 6. One of the sides and the corresponding height of a parallelogram are 4 cm and 3 cm respectively. Find the area of the parallelogram (Fig 11.17).
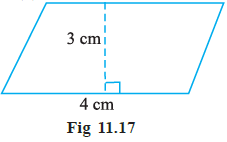
Answer:
Given:
Shape: Parallelogram
Length of one side (base, b) = 4 cm
Corresponding height (h) = 3 cm
To Find:
Area of the parallelogram.
Solution:
The formula for the area of a parallelogram is given by:
$Area \ = \ base \ \times \ height$
$A \ = \ b \ \times \ h$
Substitute the given values of the base and the corresponding height:
$A \ = \ 4 \ cm \ \times \ 3 \ cm$
$A \ = \ 12 \ cm^2$
The area of the parallelogram is 12 cm2.
Final Answer:
The area of the parallelogram is 12 cm2.
Example 7. Find the height ‘x’ if the area of the parallelogram is 24 cm2 and the base is 4 cm.
Answer:
Given:
Shape: Parallelogram
Area of the parallelogram (A) = 24 cm2
Base of the parallelogram (b) = 4 cm
Height corresponding to the base (h) = x
To Find:
The height 'x' of the parallelogram.
Solution:
The formula for the area of a parallelogram is:
$Area \ = \ base \ \times \ height$
$A \ = \ b \ \times \ h$
Substitute the given values:
$24 \ cm^2 \ = \ 4 \ cm \ \times \ x$
To find the height (x), rearrange the formula:
$x \ = \ \frac{Area}{base}$
$x \ = \ \frac{24 \ cm^2}{4 \ cm}$
$x \ = \ 6 \ cm$
The height 'x' of the parallelogram is 6 cm.
Final Answer:
The height 'x' is 6 cm.
Example 8. The two sides of the parallelogram ABCD are 6 cm and 4 cm. The height corresponding to the base CD is 3 cm (Fig 11.19). Find the
(i) area of the parallelogram.
(ii) the height corresponding to the base AD.
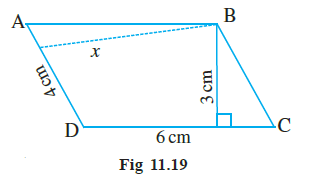
Answer:
Given:
The parallelogram is ABCD.
Length of side CD (base) = 6 cm
Length of side AD (base) = 4 cm
Height corresponding to the base CD = 3 cm
Let the height corresponding to the base AD be 'x'.
To Find:
(i) The area of the parallelogram ABCD.
(ii) The height corresponding to the base AD (i.e., the value of x).
Solution:
(i) Area of the parallelogram
The formula for the area of a parallelogram is given by:
$Area = Base \times Height$
Here, we have the base CD and its corresponding height.
Base = CD = 6 cm
Height = 3 cm
Area of parallelogram ABCD = $6 \text{ cm} \times 3 \text{ cm}$
$= 18 \text{ cm}^2$
So, the area of the parallelogram is 18 cm2.
(ii) The height corresponding to the base AD
The area of the parallelogram remains the same, regardless of which side is chosen as the base.
Now, let's consider AD as the base.
Base = AD = 4 cm
Corresponding height = x
Area of parallelogram = $18 \text{ cm}^2$ (from part i)
Using the area formula again:
$Area = Base \times Height$
$18 \text{ cm}^2 = AD \times x$
$18 = 4 \times x$
To find x, we can rearrange the equation:
$x = \frac{18}{4}$
$x = 4.5 \text{ cm}$
Therefore, the height corresponding to the base AD is 4.5 cm.
Example 9. Find the area of the following triangles (Fig 11.20).

Answer:
(i) Triangle PQR
Given:
Base (b) = QR = 4 cm
Corresponding Height (h) = PS = 2 cm
Solution:
The formula for the area of a triangle is:
$Area \ = \ \frac{1}{2} \ \times \ base \ \times \ height$
$Area \ = \ \frac{1}{2} \ \times \ b \ \times \ h$
Substitute the given values:
$Area \ = \ \frac{1}{2} \ \times \ 4 \ cm \ \times \ 2 \ cm$
$Area \ = \ \frac{1}{\cancel{2}_{\;1}} \ \times \ \cancel{4}^{\;2} \ cm \ \times \ 2 \ cm$
$Area \ = \ 2 \ cm \ \times \ 2 \ cm$
$Area \ = \ 4 \ cm^2$
The area of triangle PQR is 4 cm2.
(ii) Triangle LMN
Given:
Base (b) = MN = 3 cm
Corresponding Height (h) = LO = 2 cm
Solution:
The formula for the area of a triangle is:
$Area \ = \ \frac{1}{2} \ \times \ base \ \times \ height$
$Area \ = \ \frac{1}{2} \ \times \ b \ \times \ h$
Substitute the given values:
$Area \ = \ \frac{1}{2} \ \times \ 3 \ cm \ \times \ 2 \ cm$
$Area \ = \ \frac{1}{\cancel{2}_{\;1}} \ \times \ 3 \ cm \ \times \ \cancel{2}^{\;1} \ cm$
$Area \ = \ 1 \ \times \ 3 \ cm \ \times \ 1 \ cm$
$Area \ = \ 3 \ cm^2$
The area of triangle LMN is 3 cm2.
Final Answer:
(i) Area of ∆PQR = 4 cm2
(ii) Area of ∆LMN = 3 cm2
Example 10. Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm (Fig 11.21).

Answer:
Given:
Triangle ABC
Area of ∆ABC = 36 cm2
Height corresponding to base BC (h = AD) = 3 cm
Base = BC = ?
To Find:
The length of the base BC.
Solution:
The formula for the area of a triangle is:
$Area \ = \ \frac{1}{2} \ \times \ base \ \times \ height$
$Area \ = \ \frac{1}{2} \ \times \ BC \ \times \ AD$
Substitute the given values:
$36 \ cm^2 \ = \ \frac{1}{2} \ \times \ BC \ \times \ 3 \ cm$
To find BC, first multiply both sides by 2:
$36 \ \times \ 2 \ = \ BC \ \times \ 3$
$72 \ = \ BC \ \times \ 3$
Now, divide both sides by 3:
$BC \ = \ \frac{72}{3}$
$BC \ = \ 24 \ cm$
The length of the base BC is 24 cm.
Final Answer:
The length of BC is 24 cm.
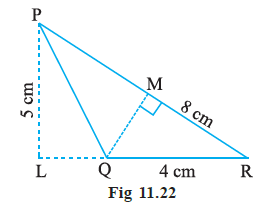
Example 11. In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm (Fig 11.22). Find:
(i) the area of the ∆PQR
(ii) QM
Answer:
Given:
Triangle PQR
Base $QR \ = \ 4$ cm
Height corresponding to base QR ($PL$) = 5 cm
Base $PR \ = \ 8$ cm
Height corresponding to base PR ($QM$) = ?
To Find:
(i) Area of the ∆PQR
(ii) Length of height QM
Solution:
(i) Area of the ∆PQR
We can calculate the area using the base QR and its corresponding height PL.
The formula for the area of a triangle is:
$Area \ = \ \frac{1}{2} \ \times \ base \ \times \ height$
Using base QR and height PL:
$Area \ = \ \frac{1}{2} \ \times \ QR \ \times \ PL$
Substitute the given values:
$Area \ = \ \frac{1}{2} \ \times \ 4 \ cm \ \times \ 5 \ cm$
$Area \ = \ \frac{1}{\cancel{2}_{\;1}} \ \times \ \cancel{4}^{\;2} \ cm \ \times \ 5 \ cm$
$Area \ = \ 2 \ cm \ \times \ 5 \ cm$
$Area \ = \ 10 \ cm^2$
The area of the ∆PQR is 10 cm2.
(ii) Finding QM
The area of the triangle remains the same regardless of which base and corresponding height are used.
We can also express the area using base PR and its corresponding height QM:
$Area \ = \ \frac{1}{2} \ \times \ PR \ \times \ QM$
We know the Area = 10 cm2 and PR = 8 cm.
$10 \ cm^2 \ = \ \frac{1}{2} \ \times \ 8 \ cm \ \times \ QM$
$10 \ cm^2 \ = \ \frac{1}{\cancel{2}_{\;1}} \ \times \ \cancel{8}^{\;4} \ cm \ \times \ QM$
$10 \ cm^2 \ = \ 4 \ cm \ \times \ QM$
To find QM, rearrange the formula:
$QM \ = \ \frac{10 \ cm^2}{4 \ cm}$
$QM \ = \ \frac{10}{4} \ cm \ = \ \frac{5}{2} \ cm$
$QM \ = \ 2.5 \ cm$
The length of the height QM is 2.5 cm.
Final Answer:
(i) The area of the ∆PQR is 10 cm2.
(ii) The length of QM is 2.5 cm.
Exercise 11.2
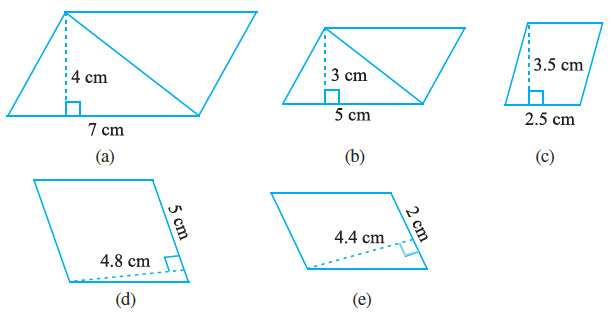
Question 1. Find the area of each of the following parallelograms:
Answer:
The formula for the area of a parallelogram is given by:
$Area \ = \ base \ \times \ corresponding \ height$
$A \ = \ b \ \times \ h$
(a)
Given:
Base (b) = 7 cm
Height (h) = 4 cm
Calculation:
$Area \ = \ 7 \ cm \ \times \ 4 \ cm \ = \ 28 \ cm^2$
Area of parallelogram (a) is 28 cm2.
(b)
Given:
Base (b) = 5 cm
Height (h) = 3 cm
Calculation:
$Area \ = \ 5 \ cm \ \times \ 3 \ cm \ = \ 15 \ cm^2$
Area of parallelogram (b) is 15 cm2.
(c)
Given:
Base (b) = 2.5 cm
Height (h) = 3.5 cm
Calculation:
$Area \ = \ 2.5 \ cm \ \times \ 3.5 \ cm \ = \ 8.75 \ cm^2$
Area of parallelogram (c) is 8.75 cm2.
(d)
Given:
Base (b) = 5 cm
Height (h) = 4.8 cm
Calculation:
$Area \ = \ 5 \ cm \ \times \ 4.8 \ cm \ = \ 24 \ cm^2$
Area of parallelogram (d) is 24 cm2.
(e)
Given:
Base (b) = 2 cm
Height (h) = 4.4 cm
Calculation:
$Area \ = \ 2 \ cm \ \times \ 4.4 \ cm \ = \ 8.8 \ cm^2$
Area of parallelogram (e) is 8.8 cm2.
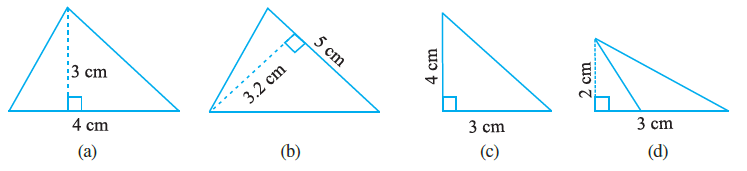
Question 2. Find the area of each of the following triangles:
Answer:
The formula for the area of a triangle is given by:
$Area \ = \ \frac{1}{2} \ \times \ base \ \times \ height$
$A \ = \ \frac{1}{2} \ b \ h$
(a)
Given:
Base (b) = 4 cm
Height (h) = 3 cm
Calculation:
$Area \ = \ \frac{1}{2} \ \times \ 4 \ cm \ \times \ 3 \ cm$
$Area \ = \ \frac{1}{\cancel{2}_{\;1}} \ \times \ \cancel{4}^{\;2} \ cm \ \times \ 3 \ cm$
$Area \ = \ 2 \ cm \ \times \ 3 \ cm \ = \ 6 \ cm^2$
Area of triangle (a) is 6 cm2.
(b)
Given:
Base (b) = 5 cm
Height (h) = 3.2 cm
Calculation:
$Area \ = \ \frac{1}{2} \ \times \ 5 \ cm \ \times \ 3.2 \ cm$
$Area \ = \ \frac{1}{2} \ \times \ 5 \ cm \ \times \ \frac{32}{10} \ cm$
$Area \ = \ \frac{1 \ \times \ 5 \ \times \ 32}{2 \ \times \ 10} \ cm^2 \ = \ \frac{160}{20} \ cm^2$
$Area \ = \ 8 \ cm^2$
Alternatively: $Area \ = \ 5 \ cm \ \times \ (\frac{1}{2} \ \times \ 3.2 \ cm) \ $$ = \ 5 \ cm \ \times \ 1.6 \ cm \ $$ = \ 8 \ cm^2$
Area of triangle (b) is 8 cm2.
(c)
Given:
Base (b) = 3 cm
Height (h) = 4 cm
Calculation:
$Area \ = \ \frac{1}{2} \ \times \ 3 \ cm \ \times \ 4 \ cm$
$Area \ = \ \frac{1}{2} \ \times \ 3 \ cm \ \times \ \cancel{4}^{\;2} \ cm$
$Area \ = \ 3 \ cm \ \times \ 2 \ cm \ = \ 6 \ cm^2$
Area of triangle (c) is 6 cm2.
(d)
Given:
Base (b) = 3 cm
Height (h) = 2 cm
Calculation:
$Area \ = \ \frac{1}{2} \ \times \ 3 \ cm \ \times \ 2 \ cm$
$Area \ = \ \frac{1}{\cancel{2}_{\;1}} \ \times \ 3 \ cm \ \times \ \cancel{2}^{\;1} \ cm$
$Area \ = \ 3 \ cm \ \times \ 1 \ cm \ = \ 3 \ cm^2$
Area of triangle (d) is 3 cm2.
Question 3. Find the missing values:
| S.No. | Base | Height | Area of the Parallelogram |
|---|---|---|---|
| a. | 20 cm | 246 cm² | |
| b. | 15 cm | 154.5 cm² | |
| c. | 8.4 cm | 48.72 cm² | |
| d. | 15.6 cm | 16.38 cm² |
Answer:
The formula for the Area of a Parallelogram is:
$Area \ = \ Base \ \times \ Height$
We can rearrange this formula to find the missing value:
$Height \ = \ \frac{Area}{Base}$
$Base \ = \ \frac{Area}{Height}$
a.
Given: Base = 20 cm, Area = 246 cm²
Missing: Height
$Height \ = \ \frac{246 \ cm^2}{20 \ cm} \ = \ 12.3 \ cm$
The missing height is 12.3 cm.
b.
Given: Height = 15 cm, Area = 154.5 cm²
Missing: Base
$Base \ = \ \frac{154.5 \ cm^2}{15 \ cm} \ = \ 10.3 \ cm$
The missing base is 10.3 cm.
c.
Given: Height = 8.4 cm, Area = 48.72 cm²
Missing: Base
$Base \ = \ \frac{48.72 \ cm^2}{8.4 \ cm} \ = \ 5.8 \ cm$
The missing base is 5.8 cm.
d.
Given: Base = 15.6 cm, Area = 16.38 cm²
Missing: Height
$Height \ = \ \frac{16.38 \ cm^2}{15.6 \ cm} \ = \ 1.05 \ cm$
The missing height is 1.05 cm.
Completed Table:
| S.No. | Base | Height | Area of the Parallelogram |
|---|---|---|---|
| a. | 20 cm | 12.3 cm | 246 cm² |
| b. | 10.3 cm | 15 cm | 154.5 cm² |
| c. | 5.8 cm | 8.4 cm | 48.72 cm² |
| d. | 15.6 cm | 1.05 cm | 16.38 cm² |
Question 4. Find the missing values:
| Base | Height | Area of Triangle |
|---|---|---|
| 15 cm | ______ | 87 cm² |
| ______ | 31.4 mm | 1256 mm² |
| 22 cm | ______ | 170.5 cm² |
Answer:
The formula for the Area of a Triangle is:
$Area \ = \ \frac{1}{2} \ \times \ Base \ \times \ Height$
We can rearrange this formula to find the missing value:
$Height \ = \ \frac{2 \ \times \ Area}{Base}$
$Base \ = \ \frac{2 \ \times \ Area}{Height}$
Row 1:
Given: Base = 15 cm, Area = 87 cm²
Missing: Height
$Height \ = \ \frac{2 \ \times \ 87 \ cm^2}{15 \ cm} \ = \ \frac{174}{15} \ cm \ = \ 11.6 \ cm$
The missing height is 11.6 cm.
Row 2:
Given: Height = 31.4 mm, Area = 1256 mm²
Missing: Base
$Base \ = \ \frac{2 \ \times \ 1256 \ mm^2}{31.4 \ mm} \ = \ \frac{2512}{31.4} \ mm$
$Base \ = \ \frac{25120}{314} \ mm \ = \ 80 \ mm$
The missing base is 80 mm.
Row 3:
Given: Base = 22 cm, Area = 170.5 cm²
Missing: Height
$Height \ = \ \frac{2 \ \times \ 170.5 \ cm^2}{22 \ cm} \ = \ \frac{341}{22} \ cm$
$Height \ = \ 15.5 \ cm$
The missing height is 15.5 cm.
Completed Table:
| Base | Height | Area of Triangle |
|---|---|---|
| 15 cm | 11.6 cm | 87 cm² |
| 80 mm | 31.4 mm | 1256 mm² |
| 22 cm | 15.5 cm | 170.5 cm² |
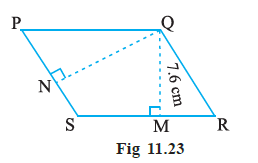
Question 5. PQRS is a parallelogram (Fig 11.23). QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
(a) the area of the parallegram PQRS
(b) QN, if PS = 8 cm
Answer:
Given:
Parallelogram PQRS.
Base SR = 12 cm.
Height QM (corresponding to base SR) = 7.6 cm.
Base PS = 8 cm.
Height QN (corresponding to base PS) = ?
To Find:
(a) Area of the parallelogram PQRS.
(b) Length of height QN.
Solution:
(a) Area of the parallelogram PQRS
The area of a parallelogram is given by the formula:
$Area \ = \ base \ \times \ corresponding \ height$
Using base SR and its corresponding height QM:
$Area \ = \ SR \ \times \ QM$
Substitute the given values:
$Area \ = \ 12 \ cm \ \times \ 7.6 \ cm$
$Area \ = \ 91.2 \ cm^2$
The area of the parallelogram PQRS is 91.2 cm2.
(b) Finding QN
The area of the parallelogram can also be calculated using the base PS and its corresponding height QN.
$Area \ = \ PS \ \times \ QN$
We already found the area to be 91.2 cm2, and we are given PS = 8 cm.
$91.2 \ cm^2 \ = \ 8 \ cm \ \times \ QN$
To find QN, rearrange the formula:
$QN \ = \ \frac{Area}{PS}$
$QN \ = \ \frac{91.2 \ cm^2}{8 \ cm}$
$QN \ = \ 11.4 \ cm$
The length of the height QN is 11.4 cm.
Final Answer:
(a) The area of parallelogram PQRS is 91.2 cm2.
(b) The length of QN is 11.4 cm.
Question 6. DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD (Fig 11.24). If the area of the parallelogram is 1470 cm2 , AB = 35 cm and AD = 49 cm, find the length of BM and DL.
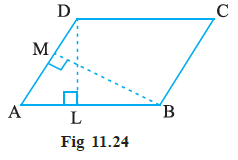
Answer:
Given:
Parallelogram ABCD.
Area of parallelogram = 1470 cm2.
Base AB = 35 cm.
Base AD = 49 cm.
DL is the height corresponding to base AB.
BM is the height corresponding to base AD.
To Find:
1. Length of height DL.
2. Length of height BM.
Solution:
The formula for the area of a parallelogram is:
$Area \ = \ base \ \times \ corresponding \ height$
1. Finding the length of DL
We use the base AB and its corresponding height DL.
$Area \ = \ AB \ \times \ DL$
Substitute the given values:
$1470 \ cm^2 \ = \ 35 \ cm \ \times \ DL$
To find DL, rearrange the formula:
$DL \ = \ \frac{Area}{AB}$
$DL \ = \ \frac{1470 \ cm^2}{35 \ cm}$
$DL \ = \ 42 \ cm$
The length of the height DL is 42 cm.
2. Finding the length of BM
Now, we use the base AD and its corresponding height BM.
$Area \ = \ AD \ \times \ BM$
Substitute the given values:
$1470 \ cm^2 \ = \ 49 \ cm \ \times \ BM$
To find BM, rearrange the formula:
$BM \ = \ \frac{Area}{AD}$
$BM \ = \ \frac{1470 \ cm^2}{49 \ cm}$
$BM \ = \ 30 \ cm$
The length of the height BM is 30 cm.
Final Answer:
The length of DL is 42 cm and the length of BM is 30 cm.
Question 7. ∆ABC is right angled at A (Fig 11.25). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ∆ABC. Also find the length of AD.

Answer:
Given:
∆ABC is right-angled at A ($m\angle BAC \ = \ 90°$).
Side AB = 5 cm.
Side AC = 12 cm.
Hypotenuse BC = 13 cm.
AD is perpendicular to BC (AD is the height corresponding to base BC).
To Find:
1. Area of ∆ABC.
2. Length of AD.
Solution:
1. Finding the Area of ∆ABC
Since ∆ABC is right-angled at A, we can consider the sides containing the right angle (AB and AC) as the base and height.
Let Base = AB = 5 cm
Let Height = AC = 12 cm
The formula for the area of a triangle is:
$Area \ = \ \frac{1}{2} \ \times \ base \ \times \ height$
$Area_{ABC} \ = \ \frac{1}{2} \ \times \ AB \ \times \ AC$
Substitute the given values:
$Area_{ABC} \ = \ \frac{1}{2} \ \times \ 5 \ cm \ \times \ 12 \ cm$
$Area_{ABC} \ = \ \frac{1}{2} \ \times \ 60 \ cm^2$
$Area_{ABC} \ = \ 30 \ cm^2$
The area of ∆ABC is 30 cm2.
2. Finding the length of AD
The area of the triangle can also be calculated using the base BC and its corresponding height AD.
$Area \ = \ \frac{1}{2} \ \times \ base \ \times \ height$
$Area_{ABC} \ = \ \frac{1}{2} \ \times \ BC \ \times \ AD$
We know the Area = 30 cm2 and BC = 13 cm.
$30 \ cm^2 \ = \ \frac{1}{2} \ \times \ 13 \ cm \ \times \ AD$
To find AD, first multiply both sides by 2:
$30 \ \times \ 2 \ = \ 13 \ \times \ AD$
$60 \ = \ 13 \ \times \ AD$
Now, divide both sides by 13:
$AD \ = \ \frac{60}{13} \ cm$
The length of AD is $\frac{60}{13}$ cm (or approximately 4.62 cm).
Final Answer:
The area of ∆ABC is 30 cm2.
The length of AD is $\frac{60}{13}$ cm.
Question 8. ∆ABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (Fig 11.26). The height AD from A to BC, is 6 cm. Find the area of ∆ABC. What will be the height from C to AB i.e., CE?
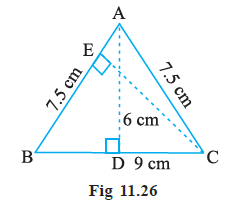
Answer:
Given:
Isosceles triangle ABC.
AB = AC = 7.5 cm.
Base BC = 9 cm.
Height AD (corresponding to base BC) = 6 cm.
Base AB = 7.5 cm.
CE is the height corresponding to base AB.
To Find:
1. Area of ∆ABC.
2. Length of height CE.
Solution:
1. Finding the Area of ∆ABC
We can calculate the area using the base BC and its corresponding height AD.
The formula for the area of a triangle is:
$Area \ = \ \frac{1}{2} \ \times \ base \ \times \ height$
Using base BC and height AD:
$Area_{ABC} \ = \ \frac{1}{2} \ \times \ BC \ \times \ AD$
Substitute the given values:
$Area_{ABC} \ = \ \frac{1}{2} \ \times \ 9 \ cm \ \times \ 6 \ cm$
$Area_{ABC} \ = \ \frac{1}{2} \ \times \ 54 \ cm^2$
$Area_{ABC} \ = \ 27 \ cm^2$
The area of ∆ABC is 27 cm2.
2. Finding the length of CE
The area of the triangle remains the same regardless of which base and corresponding height are used.
We can also express the area using base AB and its corresponding height CE:
$Area \ = \ \frac{1}{2} \ \times \ base \ \times \ height$
$Area_{ABC} \ = \ \frac{1}{2} \ \times \ AB \ \times \ CE$
We know the Area = 27 cm2 and AB = 7.5 cm.
$27 \ cm^2 \ = \ \frac{1}{2} \ \times \ 7.5 \ cm \ \times \ CE$
First, multiply both sides by 2:
$27 \ \times \ 2 \ = \ 7.5 \ \times \ CE$
$54 \ = \ 7.5 \ \times \ CE$
Now, divide both sides by 7.5 to find CE:
$CE \ = \ \frac{54}{7.5} \ cm$
$CE \ = \ \frac{540}{75} \ cm$
Simplify the fraction (divide numerator and denominator by 15):
$CE \ = \ \frac{36}{5} \ cm$
$CE \ = \ 7.2 \ cm$
The length of the height CE is 7.2 cm.
Final Answer:
The area of ∆ABC is 27 cm2.
The height from C to AB (CE) is 7.2 cm.
Example 12 to 19 (Before Exercise 11.3)
Example 12. What is the circumference of a circle of diameter 10cm (Take π = 3.14)?
Answer:
Given:
Diameter of the circle (d) = 10 cm
Value of $\pi$ to be used = 3.14
To Find:
The circumference of the circle (C).
Solution:
The formula for the circumference of a circle, given its diameter, is:
$C \ = \ \pi \ \times \ d$
Substitute the given values into the formula:
$C \ = \ 3.14 \ \times \ 10 \ cm$
$C \ = \ 31.4 \ cm$
The circumference of the circle is 31.4 cm.
Final Answer:
The circumference of the circle is 31.4 cm.
Example 13. What is the circumference of a circular disc of radius 14 cm? $\left(Use \;\pi =\frac{22}{7} \right)$
Answer:
Given:
Radius of the circular disc (r) = 14 cm
Value of $\pi$ to be used = $\frac{22}{7}$
To Find:
The circumference of the circular disc (C).
Solution:
The formula for the circumference of a circle, given its radius, is:
$C \ = \ 2 \pi r$
Substitute the given values into the formula:
$C \ = \ 2 \ \times \ \frac{22}{7} \ \times \ 14 \ cm$
Perform the calculation, cancelling the common factor of 7:
$C \ = \ 2 \ \times \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{14}^2 \ cm$
$C \ = \ 2 \ \times \ 22 \ \times \ 2 \ cm$
$C \ = \ 44 \ \times \ 2 \ cm$
$C \ = \ 88 \ cm$
The circumference of the circular disc is 88 cm.
Final Answer:
The circumference of the circular disc is 88 cm.
Example 14. The radius of a circular pipe is 10 cm. What length of a tape is required to wrap once around the pipe (π = 3.14)?
Answer:
Given:
Radius of the circular pipe (r) = 10 cm
Value of $\pi$ to be used = 3.14
To Find:
The length of tape required to wrap once around the pipe.
Solution:
The length of tape required to wrap once around the circular pipe is equal to the circumference of the pipe.
The formula for the circumference of a circle, given its radius, is:
$C \ = \ 2 \pi r$
Substitute the given values into the formula:
$C \ = \ 2 \ \times \ 3.14 \ \times \ 10 \ cm$
$C \ = \ 6.28 \ \times \ 10 \ cm$
$C \ = \ 62.8 \ cm$
The length of tape required is 62.8 cm.
Final Answer:
The length of tape required is 62.8 cm.
Example 15. Find the perimeter of the given shape (Fig 11.32) $\left(Take \;\pi =\frac{22}{7} \right)$?

Answer:
Given:
The shape consists of four semi-circular arcs.
The diameter of each semi-circle (d) = 14 cm.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
The perimeter of the given shape.
Solution:
The perimeter of the shape is the total length of the four semi-circular arcs.
First, find the radius (r) of each semi-circle:
$r \ = \ \frac{diameter}{2} \ = \ \frac{14 \ cm}{2} \ = \ 7 \ cm$
Next, find the length of one semi-circular arc. The length of a semi-circular arc is half the circumference of a full circle with the same radius.
Circumference of a full circle = $2 \pi r$
Length of one semi-circular arc = $\frac{1}{2} \ \times \ 2 \pi r \ = \ \pi r$
Substitute the values of $\pi$ and r:
Length of one arc = $\frac{22}{7} \ \times \ 7 \ cm$
Length of one arc = $\frac{22}{\cancel{7}_1} \ \times \ \cancel{7}^1 \ cm \ = \ 22 \ cm$
The perimeter of the entire shape is the sum of the lengths of the four identical semi-circular arcs.
Total Perimeter = $4 \ \times$ (Length of one arc)
Total Perimeter = $4 \ \times \ 22 \ cm$
Total Perimeter = $88 \ cm$
The perimeter of the given shape is 88 cm.
Final Answer:
The perimeter of the shape is 88 cm.
Example 16. Sudhanshu divides a circular disc of radius 7 cm in two equal parts. What is the perimeter of each semicircular shape disc? $\left(Use \;\pi =\frac{22}{7} \right)$
Answer:
Given:
A circular disc is divided into two equal semi-circular parts.
Radius of the original circular disc (r) = 7 cm
Value of $\pi$ to be used = $\frac{22}{7}$
To Find:
The perimeter of one semi-circular shape disc.
Solution:
The perimeter of a semi-circular disc consists of two parts:
1. The length of the curved semi-circular arc.
2. The length of the straight diameter.
Step 1: Calculate the length of the semi-circular arc
The length of the semi-circular arc is half the circumference of the full circle.
Circumference of full circle = $2 \pi r$
Length of semi-circular arc = $\frac{1}{2} \ \times \ 2 \pi r \ = \ \pi r$
Substitute the given values:
Length of arc = $\frac{22}{7} \ \times \ 7 \ cm$
Length of arc = $\frac{22}{\cancel{7}_1} \ \times \ \cancel{7}^1 \ cm \ = \ 22 \ cm$
Step 2: Calculate the length of the diameter
The diameter (d) is twice the radius.
$d \ = \ 2r$
$d \ = \ 2 \ \times \ 7 \ cm \ = \ 14 \ cm$
Step 3: Calculate the perimeter of the semi-circular disc
Perimeter = Length of semi-circular arc + Length of diameter
Perimeter = $22 \ cm \ + \ 14 \ cm$
Perimeter = $36 \ cm$
The perimeter of each semi-circular shape disc is 36 cm.
Final Answer:
The perimeter of each semi-circular shape disc is 36 cm.
Example 17. Find the area of a circle of radius 30 cm (use π = 3.14).
Answer:
Given:
Radius of the circle (r) = 30 cm
Value of $\pi$ to be used = 3.14
To Find:
The area of the circle (A).
Solution:
The formula for the area of a circle is:
$A \ = \ \pi r^2$
Substitute the given values into the formula:
$A \ = \ 3.14 \ \times \ (30 \ cm)^2$
$A \ = \ 3.14 \ \times \ (30 \ cm \ \times \ 30 \ cm)$
$A \ = \ 3.14 \ \times \ 900 \ cm^2$
Or, $3.14 \ \times \ 900 \ = \ 314 \ \times \ 9 \ = \ 2826$.
$A \ = \ 2826 \ cm^2$
The area of the circle is 2826 cm2.
Final Answer:
The area of the circle is 2826 cm2.
Example 18. Diameter of a circular garden is 9.8 m. Find its area.
Answer:
Given:
Diameter of the circular garden (d) = 9.8 m
(We will use $\pi \ = \ \frac{22}{7}$ as 9.8 is a multiple of 7)
To Find:
The area of the circular garden (A).
Solution:
First, find the radius (r) of the circular garden:
$Radius \ (r) \ = \ \frac{Diameter}{2} \ = \ \frac{d}{2}$
$r \ = \ \frac{9.8 \ m}{2} \ = \ 4.9 \ m$
Now, use the formula for the area of a circle:
$A \ = \ \pi r^2$
Substitute the value of the radius and $\pi \ = \ \frac{22}{7}$:
$A \ = \ \frac{22}{7} \ \times \ (4.9 \ m)^2$
$A \ = \ \frac{22}{7} \ \times \ (4.9 \ m) \ \times \ (4.9 \ m)$
Perform the calculation:
$A \ = \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{4.9}^{0.7} \ m \ \times \ 4.9 \ m$
$A \ = \ 22 \ \times \ 0.7 \ m \ \times \ 4.9 \ m$
$A \ = \ 15.4 \ m \ \times \ 4.9 \ m$
$A \ = \ 75.46 \ m^2$
The area of the circular garden is 75.46 m2.
Final Answer:
The area of the circular garden is 75.46 m2.
Example 19. The adjoining figure shows two circles with the same centre. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm

Answer:
Given:
Two circles with the same centre (concentric circles).
Radius of the larger circle (R) = 10 cm
Radius of the smaller circle (r) = 4 cm
Value of $\pi$ to be used = 3.14
To Find:
(a) Area of the larger circle ($A_{larger}$)
(b) Area of the smaller circle ($A_{smaller}$)
(c) Area of the shaded region between the circles ($A_{shaded}$)
Solution:
(a) Area of the larger circle
The formula for the area of a circle is $A \ = \ \pi \times (Radius)^2$.
$A_{larger} \ = \ \pi R^2$
$A_{larger} \ = \ 3.14 \ \times \ (10 \ cm)^2$
$A_{larger} \ = \ 3.14 \ \times \ 100 \ cm^2$
$A_{larger} \ = \ 314 \ cm^2$
The area of the larger circle is 314 cm2.
(b) Area of the smaller circle
$A_{smaller} \ = \ \pi r^2$
$A_{smaller} \ = \ 3.14 \ \times \ (4 \ cm)^2$
$A_{smaller} \ = \ 3.14 \ \times \ 16 \ cm^2$
$A_{smaller} \ = \ 50.24 \ cm^2$
The area of the smaller circle is 50.24 cm2.
(c) Area of the shaded region
The area of the shaded region is the difference between the area of the larger circle and the area of the smaller circle.
$A_{shaded} \ = \ A_{larger} \ - \ A_{smaller}$
$A_{shaded} \ = \ 314 \ cm^2 \ - \ 50.24 \ cm^2$
$A_{shaded} \ = \ 263.76 \ cm^2$
The area of the shaded region is 263.76 cm2.
Final Answer:
(a) Area of the larger circle = 314 cm2
(b) Area of the smaller circle = 50.24 cm2
(c) Area of the shaded region = 263.76 cm2
Exercise 11.3
Question 1. Find the circumference of the circles with the following radius: $\left(Take \;\pi =\frac{22}{7} \right)$
(a) 14 cm
(b) 28 mm
(c) 21 cm
Answer:
The formula for the circumference of a circle given its radius (r) is:
$Circumference \ (C) \ = \ 2 \pi r$
We are given $\pi \ = \ \frac{22}{7}$.
(a) Radius (r) = 14 cm
$C \ = \ 2 \ \times \ \frac{22}{7} \ \times \ 14 \ cm$
$C \ = \ 2 \ \times \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{14}^2 \ cm$
$C \ = \ 2 \ \times \ 22 \ \times \ 2 \ cm$
$C \ = \ 88 \ cm$
The circumference of the circle with radius 14 cm is 88 cm.
(b) Radius (r) = 28 mm
$C \ = \ 2 \ \times \ \frac{22}{7} \ \times \ 28 \ mm$
$C \ = \ 2 \ \times \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{28}^4 \ mm$
$C \ = \ 2 \ \times \ 22 \ \times \ 4 \ mm$
$C \ = \ 44 \ \times \ 4 \ mm$
$C \ = \ 176 \ mm$
The circumference of the circle with radius 28 mm is 176 mm.
(c) Radius (r) = 21 cm
$C \ = \ 2 \ \times \ \frac{22}{7} \ \times \ 21 \ cm$
$C \ = \ 2 \ \times \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{21}^3 \ cm$
$C \ = \ 2 \ \times \ 22 \ \times \ 3 \ cm$
$C \ = \ 44 \ \times \ 3 \ cm$
$C \ = \ 132 \ cm$
The circumference of the circle with radius 21 cm is 132 cm.
Question 2. Find the area of the following circles, given that:
(a) radius = 14 mm $\left(Take \;\pi =\frac{22}{7} \right)$
(b) diameter = 49 m
(c) radius = 5 cm
Answer:
The formula for the area of a circle given its radius (r) is:
$Area \ (A) \ = \ \pi r^2$
(a) radius = 14 mm $\left(Take \;\pi \ = \ \frac{22}{7} \right)$
Given:
Radius (r) = 14 mm
$\pi \ = \ \frac{22}{7}$
Calculation:
$A \ = \ \pi r^2 \ = \ \frac{22}{7} \ \times \ (14 \ mm)^2$
$A \ = \ \frac{22}{7} \ \times \ 14 \ mm \ \times \ 14 \ mm$
$A \ = \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{14}^2 \ mm \ \times \ 14 \ mm$
$A \ = \ 22 \ \times \ 2 \ mm \ \times \ 14 \ mm$
$A \ = \ 44 \ mm \ \times \ 14 \ mm$
$A \ = \ 616 \ mm^2$
The area of the circle is 616 mm2.
(b) diameter = 49 m
Given:
Diameter (d) = 49 m
(We will use $\pi \ = \ \frac{22}{7}$)
Calculation:
First, find the radius (r):
$r \ = \ \frac{Diameter}{2} \ = \ \frac{49}{2} \ m$
Now, calculate the area:
$A \ = \ \pi r^2 \ = \ \frac{22}{7} \ \times \ \left( \frac{49}{2} \ m \right)^2$
$A \ = \ \frac{22}{7} \ \times \ \frac{49}{2} \ m \ \times \ \frac{49}{2} \ m$
$A \ = \ \frac{\cancel{22}^{11}}{\cancel{7}_1} \ \times \ \frac{\cancel{49}^7}{\cancel{2}_1} \ m \ \times \ \frac{49}{2} \ m$
$A \ = \ 11 \ \times \ 7 \ m \ \times \ \frac{49}{2} \ m$
$A \ = \ 77 \ m \ \times \ \frac{49}{2} \ m$
$A \ = \ \frac{77 \ \times \ 49}{2} \ m^2 \ = \ \frac{3773}{2} \ m^2$
$A \ = \ 1886.5 \ m^2$
The area of the circle is 1886.5 m2.
(c) radius = 5 cm
Given:
Radius (r) = 5 cm
(We will use $\pi \ = \ \frac{22}{7}$)
Calculation:
$A \ = \ \pi r^2 \ = \ \frac{22}{7} \ \times \ (5 \ cm)^2$
$A \ = \ \frac{22}{7} \ \times \ 25 \ cm^2$
$A \ = \ \frac{22 \ \times \ 25}{7} \ cm^2 \ = \ \frac{550}{7} \ cm^2$
$A \ \approx \ 78.57 \ cm^2$
The area of the circle is $\frac{550}{7}$ cm2 (or approximately 78.57 cm2).
(If $\pi = 3.14$ is used: $A \ = \ 3.14 \ \times \ (5 \ cm)^2 \ $$ = \ 3.14 \ \times \ 25 \ cm^2 \ $$ = \ 78.5 \ cm^2$)
Question 3. If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet. $\left(Take \;\pi =\frac{22}{7} \right)$
Answer:
Given:
Circumference of the circular sheet (C) = 154 m
Value of $\pi$ to be used = $\frac{22}{7}$
To Find:
1. Radius of the circular sheet (r)
2. Area of the circular sheet (A)
Solution:
Step 1: Find the radius (r)
The formula for the circumference of a circle is:
$C \ = \ 2 \pi r$
Substitute the given values:
$154 \ m \ = \ 2 \ \times \ \frac{22}{7} \ \times \ r$
$154 \ m \ = \ \frac{44}{7} \ \times \ r$
To find the radius (r), rearrange the formula:
$r \ = \ 154 \ m \ \times \ \frac{7}{44}$
Simplify the calculation:
$r \ = \ \frac{\cancel{154}^{7}}{\cancel{44}_2} \ \times \ 7 \ m$ (Divide 154 and 44 by 22)
$r \ = \ \frac{7 \ \times \ 7}{2} \ m$
$r \ = \ \frac{49}{2} \ m \ = \ 24.5 \ m$
The radius of the circular sheet is 24.5 m.
Step 2: Find the area (A)
The formula for the area of a circle is:
$A \ = \ \pi r^2$
Substitute the value of $\pi$ and the calculated radius:
$A \ = \ \frac{22}{7} \ \times \ (24.5 \ m)^2$
$A \ = \ \frac{22}{7} \ \times \ \left( \frac{49}{2} \ m \right)^2$
$A \ = \ \frac{22}{7} \ \times \ \frac{49}{2} \ m \ \times \ \frac{49}{2} \ m$
Simplify the calculation:
$A \ = \ \frac{\cancel{22}^{11}}{\cancel{7}_1} \ \times \ \frac{\cancel{49}^7}{\cancel{2}_1} \ m \ \times \ \frac{49}{2} \ m$
$A \ = \ 11 \ \times \ 7 \ m \ \times \ \frac{49}{2} \ m$
$A \ = \ 77 \ m \ \times \ \frac{49}{2} \ m$
$A \ = \ \frac{77 \ \times \ 49}{2} \ m^2$
$A \ = \ \frac{3773}{2} \ m^2$
$A \ = \ 1886.5 \ m^2$
The area of the circular sheet is 1886.5 m2.
Final Answer:
The radius of the circular sheet is 24.5 m and its area is 1886.5 m2.
Question 4. A gardener wants to fence a circular garden of diameter 21m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the cost of the rope, if it costs ₹ 4 per meter. $\left(Take \;\pi =\frac{22}{7} \right)$
Answer:
Given:
Shape of the garden = Circular
Diameter of the garden (d) = 21 m
Number of rounds of fence = 2
Cost rate of rope =
Value of $\pi$ to be used = $\frac{22}{7}$
To Find:
1. Total length of the rope needed.
2. Total cost of the rope.
Solution:
Step 1: Find the length of rope for one round (Circumference)
The length of rope required for one round of fence is equal to the circumference of the circular garden.
The formula for the circumference of a circle, given its diameter, is:
$Circumference \ (C) \ = \ \pi d$
Substitute the given values:
$C \ = \ \frac{22}{7} \ \times \ 21 \ m$
$C \ = \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{21}^3 \ m$
$C \ = \ 22 \ \times \ 3 \ m$
$C \ = \ 66 \ m$
The length of rope needed for one round is 66 m.
Step 2: Find the total length of rope needed for 2 rounds
The gardener makes 2 rounds of fence.
Total length of rope = Circumference $\times$ Number of rounds
Total length = $66 \ m \ \times \ 2$
Total length = $132 \ m$
The total length of rope the gardener needs to purchase is 132 m.
Step 3: Find the total cost of the rope
The cost of the rope is
Total Cost = Total length of rope $\times$ Cost per meter
Total Cost = $132 \ m \ \times \ \textsf{₹} 4 / m$
Total Cost =
Total Cost =
The total cost of the rope is
Final Answer:
The total length of rope needed is 132 m.
The total cost of the rope is
Question 5. From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Answer:
Given:
Radius of the original circular sheet (R) = 4 cm.
Radius of the removed circle (r) = 3 cm.
Value of $\pi$ to be used = 3.14.
To Find:
The area of the remaining sheet.
Solution:
The area of the remaining sheet is the difference between the area of the original larger circular sheet and the area of the removed smaller circle.
Step 1: Calculate the area of the original circular sheet (Larger Circle)
The formula for the area of a circle is $A \ = \ \pi \times (Radius)^2$.
$Area_{larger} \ = \ \pi R^2$
$Area_{larger} \ = \ 3.14 \ \times \ (4 \ cm)^2$
$Area_{larger} \ = \ 3.14 \ \times \ 16 \ cm^2$
$Area_{larger} \ = \ 50.24 \ cm^2$
Step 2: Calculate the area of the removed circle (Smaller Circle)
$Area_{smaller} \ = \ \pi r^2$
$Area_{smaller} \ = \ 3.14 \ \times \ (3 \ cm)^2$
$Area_{smaller} \ = \ 3.14 \ \times \ 9 \ cm^2$
$Area_{smaller} \ = \ 28.26 \ cm^2$
Step 3: Calculate the area of the remaining sheet
Area of remaining sheet = Area of larger circle - Area of smaller circle
$Area_{remaining} \ = \ Area_{larger} \ - \ Area_{smaller}$
$Area_{remaining} \ = \ 50.24 \ cm^2 \ - \ 28.26 \ cm^2$
$Area_{remaining} \ = \ 21.98 \ cm^2$
The area of the remaining sheet is 21.98 cm2.
Alternate Solution:
We can also solve this by first factoring the formula.
Area of remaining sheet = Area of larger circle - Area of smaller circle
$Area_{remaining} \ = \ \pi R^2 - \pi r^2$
By taking $\pi$ as a common factor:
$Area_{remaining} \ = \ \pi (R^2 - r^2)$
Substitute the given values:
$Area_{remaining} \ = \ 3.14 \times ((4)^2 - (3)^2)$
$Area_{remaining} \ = \ 3.14 \times (16 - 9)$
$Area_{remaining} \ = \ 3.14 \times 7$
$Area_{remaining} \ = \ 21.98 \ cm^2$
This method gives the same result.
Final Answer:
The area of the remaining sheet is 21.98 cm2.
Question 6. Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs ₹ 15. (Take π = 3.14)
Answer:
Given:
Shape of the table cover = Circular
Diameter of the table cover (d) = 1.5 m
Cost rate of lace =
Value of $\pi$ to be used = 3.14
To Find:
1. Length of the lace required.
2. Total cost of the lace.
Solution:
Step 1: Find the length of lace required (Circumference)
The length of lace required to go around the edge of the circular table cover is equal to its circumference.
The formula for the circumference of a circle, given its diameter, is:
$Circumference \ (C) \ = \ \pi d$
Substitute the given values:
$C \ = \ 3.14 \ \times \ 1.5 \ m$
$C \ = \ 4.71 \ m$
The length of the lace required is 4.71 m.
Step 2: Find the total cost of the lace
The cost of the lace is
Total Cost = Length of lace $\times$ Cost per meter
Total Cost = $4.71 \ m \ \times \ \textsf{₹} 15 / m$
Total Cost =
Total Cost =
The total cost of the lace is
Final Answer:
The length of the lace required is 4.71 m.
The total cost of the lace is
Question 7. Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
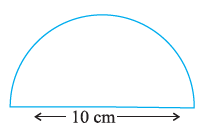
Answer:
Given:
The figure shows a semi-circle.
Diameter of the semi-circle (d) = 10 cm.
(We will use $\pi \ = \ \frac{22}{7}$ unless specified otherwise)
To Find:
The perimeter of the semi-circle including its diameter.
Solution:
The perimeter of the shape consists of two parts:
1. The length of the curved semi-circular arc.
2. The length of the straight diameter.
Step 1: Calculate the radius (r)
$r \ = \ \frac{diameter}{2} \ = \ \frac{10 \ cm}{2} \ = \ 5 \ cm$
Step 2: Calculate the length of the semi-circular arc
The length of the semi-circular arc is half the circumference of a full circle with the same radius.
Circumference of full circle = $2 \pi r$
Length of semi-circular arc = $\frac{1}{2} \ \times \ 2 \pi r \ = \ \pi r$
Substitute the values of $\pi$ and r:
Length of arc = $\frac{22}{7} \ \times \ 5 \ cm$
Length of arc = $\frac{110}{7} \ cm$
Step 3: Calculate the perimeter of the shape
Perimeter = Length of semi-circular arc + Length of diameter
Perimeter = $\frac{110}{7} \ cm \ + \ 10 \ cm$
To add these, find a common denominator:
Perimeter = $\frac{110}{7} \ cm \ + \ \frac{10 \ \times \ 7}{7} \ cm$
Perimeter = $\frac{110}{7} \ cm \ + \ \frac{70}{7} \ cm$
Perimeter = $\frac{110 \ + \ 70}{7} \ cm$
Perimeter = $\frac{180}{7} \ cm$
The perimeter of the shape is $\frac{180}{7}$ cm (or approximately 25.71 cm).
Final Answer:
The perimeter of the figure is $\frac{180}{7}$ cm.
Question 8. Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2 . (Take π = 3.14)
Answer:
Given:
Shape of the table-top = Circular
Diameter of the table-top (d) = 1.6 m
Rate of polishing =
Value of $\pi$ to be used = 3.14
To Find:
The total cost of polishing the circular table-top.
Solution:
Step 1: Calculate the radius (r) of the table-top
The radius is half the diameter.
$r \ = \ \frac{Diameter}{2} \ = \ \frac{1.6 \ m}{2} \ = \ 0.8 \ m$
Step 2: Calculate the area of the table-top
The area of a circle is given by the formula:
$Area \ (A) \ = \ \pi r^2$
Substitute the values of $\pi$ and the calculated radius:
$A \ = \ 3.14 \ \times \ (0.8 \ m)^2$
$A \ = \ 3.14 \ \times \ (0.8 \ m \ \times \ 0.8 \ m)$
$A \ = \ 3.14 \ \times \ 0.64 \ m^2$
$A \ = \ 2.0096 \ m^2$
The area of the circular table-top is 2.0096 m2.
Step 3: Calculate the total cost of polishing
The cost is calculated by multiplying the total area by the rate per square meter.
Total Cost = Area $\times$ Rate of polishing
Total Cost = $2.0096 \ m^2 \ \times \ \textsf{₹} 15 / m^2$
Total Cost =
Total Cost =
The total cost of polishing the table-top is
Final Answer:
The cost of polishing the circular table-top is
Question 9. Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? $\left(Take \;\pi =\frac{22}{7} \right)$
Answer:
Given:
Total length of the wire = 44 cm.
Shape 1: Circle (formed using the wire).
Shape 2: Square (formed using the same wire).
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
1. Radius of the circle (r).
2. Area of the circle ($A_{circle}$).
3. Length of each side of the square (s).
4. Which figure (circle or square) encloses more area?
Solution:
Part 1: Calculations for the Circle
When the wire is bent into a circle, its length becomes the circumference of the circle.
Circumference (C) = Length of wire = 44 cm.
The formula for circumference is $C \ = \ 2 \pi r$.
Substitute the known values:
$44 \ cm \ = \ 2 \ \times \ \frac{22}{7} \ \times \ r$
$44 \ cm \ = \ \frac{44}{7} \ \times \ r$
To find the radius (r), rearrange the formula:
$r \ = \ 44 \ cm \ \times \ \frac{7}{44}$
$r \ = \ \frac{\cancel{44}^1}{\cancel{44}_1} \ \times \ 7 \ cm$
$r \ = \ 7 \ cm$
The radius of the circle is 7 cm.
Now, find the area of the circle using the formula $A \ = \ \pi r^2$.
$A_{circle} \ = \ \frac{22}{7} \ \times \ (7 \ cm)^2$
$A_{circle} \ = \ \frac{22}{7} \ \times \ 7 \ cm \ \times \ 7 \ cm$
$A_{circle} \ = \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{7}^1 \ cm \ \times \ 7 \ cm$
$A_{circle} \ = \ 22 \ \times \ 7 \ cm^2$
$A_{circle} \ = \ 154 \ cm^2$
The area of the circle is 154 cm2.
Part 2: Calculations for the Square
When the same wire is bent into a square, its length becomes the perimeter of the square.
Perimeter (P) = Length of wire = 44 cm.
Let the side of the square be 's'. The formula for the perimeter of a square is $P \ = \ 4s$.
Substitute the known perimeter:
$44 \ cm \ = \ 4s$
To find the side (s), divide the perimeter by 4:
$s \ = \ \frac{44 \ cm}{4}$
$s \ = \ 11 \ cm$
The length of each side of the square is 11 cm.
Now, find the area of the square using the formula $A \ = \ s^2$.
$A_{square} \ = \ (11 \ cm)^2$
$A_{square} \ = \ 11 \ cm \ \times \ 11 \ cm$
$A_{square} \ = \ 121 \ cm^2$
The area of the square is 121 cm2.
Part 3: Comparison of Areas
Area of the circle = 154 cm2.
Area of the square = 121 cm2.
Comparing the two areas: $154 \ cm^2 \ > \ 121 \ cm^2$.
Therefore, the circle encloses more area than the square.
Final Answer:
Radius of the circle = 7 cm.
Area of the circle = 154 cm2.
Length of each side of the square = 11 cm.
The circle encloses more area.
Question 10. From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1cm are removed. (as shown in the adjoining figure). Find the area of the remaining sheet. $\left(Take \;\pi =\frac{22}{7} \right)$

Answer:
Given:
Radius of the large circular card sheet (R) = 14 cm.
Radius of the two small circles removed (r) = 3.5 cm.
Length of the rectangle removed (l) = 3 cm.
Breadth of the rectangle removed (b) = 1 cm.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
The area of the remaining sheet.
Solution:
The area of the remaining sheet is the area of the large circular sheet minus the total area of the shapes removed (two small circles and one rectangle).
Step 1: Calculate the area of the large circular sheet
$Area_{large\_circle} \ = \ \pi R^2$
$Area_{large\_circle} \ = \ \frac{22}{7} \ \times \ (14 \ cm)^2$
$Area_{large\_circle} \ = \ \frac{22}{7} \ \times \ 14 \ cm \ \times \ 14 \ cm$
$Area_{large\_circle} \ = \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{14}^2 \ cm \ \times \ 14 \ cm$
$Area_{large\_circle} \ = \ 22 \ \times \ 2 \ cm \ \times \ 14 \ cm$
$Area_{large\_circle} \ = \ 44 \ \times \ 14 \ cm^2 \ = \ 616 \ cm^2$
Step 2: Calculate the area of one small circle
$Area_{small\_circle} \ = \ \pi r^2$
$Area_{small\_circle} \ = \ \frac{22}{7} \ \times \ (3.5 \ cm)^2$
$Area_{small\_circle} \ = \ \frac{22}{7} \ \times \ 3.5 \ cm \ \times \ 3.5 \ cm$
$Area_{small\_circle} \ = \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{3.5}^{0.5} \ cm \ \times \ 3.5 \ cm$
$Area_{small\_circle} \ = \ 22 \ \times \ 0.5 \ cm \ \times \ 3.5 \ cm$
$Area_{small\_circle} \ = \ 11 \ cm \ \times \ 3.5 \ cm \ = \ 38.5 \ cm^2$
Step 3: Calculate the total area of the two small circles
$Area_{two\_small\_circles} \ = \ 2 \ \times \ Area_{small\_circle}$
$Area_{two\_small\_circles} \ = \ 2 \ \times \ 38.5 \ cm^2 \ = \ 77 \ cm^2$
Step 4: Calculate the area of the rectangle
$Area_{rectangle} \ = \ length \ \times \ breadth \ = \ l \ \times \ b$
$Area_{rectangle} \ = \ 3 \ cm \ \times \ 1 \ cm \ = \ 3 \ cm^2$
Step 5: Calculate the total area removed
$Area_{removed} \ = \ Area_{two\_small\_circles} \ + \ Area_{rectangle}$
$Area_{removed} \ = \ 77 \ cm^2 \ + \ 3 \ cm^2 \ = \ 80 \ cm^2$
Step 6: Calculate the area of the remaining sheet
$Area_{remaining} \ = \ Area_{large\_circle} \ - \ Area_{removed}$
$Area_{remaining} \ = \ 616 \ cm^2 \ - \ 80 \ cm^2$
$Area_{remaining} \ = \ 536 \ cm^2$
Final Answer:
The area of the remaining sheet is 536 cm2.
Question 11. A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
Answer:
Given:
Shape of the aluminium sheet: Square
Side of the square sheet (s) = 6 cm
Shape cut out: Circle
Radius of the cut-out circle (r) = 2 cm
Value of $\pi$ to be used = 3.14
To Find:
The area of the leftover aluminium sheet.
Solution:
The area of the leftover sheet is the area of the original square sheet minus the area of the circle that was cut out.
Step 1: Calculate the area of the square sheet
The formula for the area of a square is:
$Area_{square} \ = \ side^2 \ = \ s^2$
Substitute the given side length:
$Area_{square} \ = \ (6 \ cm)^2$
$Area_{square} \ = \ 6 \ cm \ \times \ 6 \ cm \ = \ 36 \ cm^2$
Step 2: Calculate the area of the cut-out circle
The formula for the area of a circle is:
$Area_{circle} \ = \ \pi r^2$
Substitute the given radius and the value of $\pi$:
$Area_{circle} \ = \ 3.14 \ \times \ (2 \ cm)^2$
$Area_{circle} \ = \ 3.14 \ \times \ 4 \ cm^2$
$Area_{circle} \ = \ 12.56 \ cm^2$
Step 3: Calculate the area of the leftover aluminium sheet
Area of leftover sheet = Area of square sheet - Area of cut-out circle
$Area_{leftover} \ = \ Area_{square} \ - \ Area_{circle}$
$Area_{leftover} \ = \ 36 \ cm^2 \ - \ 12.56 \ cm^2$
$Area_{leftover} \ = \ 23.44 \ cm^2$
The area of the leftover aluminium sheet is 23.44 cm2.
Final Answer:
The area of the leftover aluminium sheet is 23.44 cm2.
Question 12. The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
Answer:
Given:
Circumference of the circle (C) = 31.4 cm
Value of $\pi$ to be used = 3.14
To Find:
1. Radius of the circle (r)
2. Area of the circle (A)
Solution:
Step 1: Find the radius (r)
The formula for the circumference of a circle is:
$C \ = \ 2 \pi r$
Substitute the given values:
$31.4 \ cm \ = \ 2 \ \times \ 3.14 \ \times \ r$
$31.4 \ cm \ = \ 6.28 \ \times \ r$
To find the radius (r), rearrange the formula:
$r \ = \ \frac{31.4 \ cm}{6.28}$
To simplify the division, we can multiply the numerator and denominator by 100:
$r \ = \ \frac{31.4 \ \times \ 100}{6.28 \ \times \ 100} \ cm \ = \ \frac{3140}{628} \ cm$
$r \ = \ 5 \ cm$
The radius of the circle is 5 cm.
Step 2: Find the area (A)
The formula for the area of a circle is:
$A \ = \ \pi r^2$
Substitute the value of $\pi$ and the calculated radius:
$A \ = \ 3.14 \ \times \ (5 \ cm)^2$
$A \ = \ 3.14 \ \times \ 25 \ cm^2$
$A \ = \ 78.5 \ cm^2$
The area of the circle is 78.5 cm2.
Final Answer:
The radius of the circle is 5 cm and its area is 78.5 cm2.
Question 13. A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
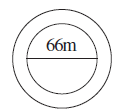
Answer:
Given:
Shape of the flower bed = Circular
Diameter of the flower bed ($d_{bed}$) = 66 m
Width of the surrounding path = 4 m
Value of $\pi$ to be used = 3.14
To Find:
The area of the path.
Solution:
The path is the region between the outer circle (flower bed + path) and the inner circle (flower bed).
Step 1: Calculate the radius of the inner circle (flower bed, r)
$r \ = \ \frac{Diameter \ of \ flower \ bed}{2} \ = \ \frac{66 \ m}{2} \ = \ 33 \ m$
Step 2: Calculate the radius of the outer circle (flower bed + path, R)
The radius of the outer circle is the radius of the flower bed plus the width of the path.
$R \ = \ Radius \ of \ flower \ bed \ + \ Width \ of \ path$
$R \ = \ 33 \ m \ + \ 4 \ m \ = \ 37 \ m$
Step 3: Calculate the area of the outer circle
The formula for the area of a circle is $Area \ = \ \pi \times (Radius)^2$.
$Area_{outer} \ = \ \pi R^2$
$Area_{outer} \ = \ 3.14 \ \times \ (37 \ m)^2$
$Area_{outer} \ = \ 3.14 \ \times \ 1369 \ m^2$
$Area_{outer} \ = \ 4298.66 \ m^2$
Step 4: Calculate the area of the inner circle (flower bed)
$Area_{inner} \ = \ \pi r^2$
$Area_{inner} \ = \ 3.14 \ \times \ (33 \ m)^2$
$Area_{inner} \ = \ 3.14 \ \times \ 1089 \ m^2$
$Area_{inner} \ = \ 3419.46 \ m^2$
Step 5: Calculate the area of the path
The area of the path is the difference between the area of the outer circle and the area of the inner circle.
$Area_{path} \ = \ Area_{outer} \ - \ Area_{inner}$
$Area_{path} \ = \ 4298.66 \ m^2 \ - \ 3419.46 \ m^2$
$Area_{path} \ = \ 879.2 \ m^2$
The area of the path is 879.2 m2.
Final Answer:
The area of the path is 879.2 m2.
Question 14. A circular flower garden has an area of 314 m2 . A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
Answer:
Given:
Area of the circular flower garden ($A_{garden}$) = 314 m2
Radius of the area covered by the sprinkler ($r_{sprinkler}$) = 12 m
Value of $\pi$ to be used = 3.14
To Determine:
Whether the sprinkler will water the entire garden.
Solution:
To determine if the sprinkler waters the entire garden, we need to compare the area the sprinkler can cover with the area of the garden.
Step 1: Calculate the area covered by the sprinkler
The area covered by the sprinkler is a circle with radius 12 m.
The formula for the area of a circle is:
$Area \ = \ \pi r^2$
$Area_{sprinkler} \ = \ \pi \ \times \ (r_{sprinkler})^2$
Substitute the given values:
$Area_{sprinkler} \ = \ 3.14 \ \times \ (12 \ m)^2$
$Area_{sprinkler} \ = \ 3.14 \ \times \ 144 \ m^2$
$Area_{sprinkler} \ = \ 452.16 \ m^2$
The sprinkler can cover an area of 452.16 m2.
Step 2: Compare the sprinkler coverage area with the garden area
Area of the garden ($A_{garden}$) = 314 m2
Area covered by the sprinkler ($Area_{sprinkler}$) = 452.16 m2
Since $452.16 \ m^2 \ > \ 314 \ m^2$, the area covered by the sprinkler is greater than the area of the garden.
Therefore, the sprinkler will water the entire garden.
Final Answer:
Yes, the sprinkler will water the entire garden because the area it covers (452.16 m2) is greater than the area of the garden (314 m2).
Question 15. Find the circumference of the inner and the outer circles, shown in the adjoining figure? (Take π = 3.14)
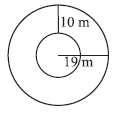
Answer:
Given:
Two concentric circles.
Radius of the outer circle (R) = 19 m.
Width of the path between the circles = 10 m.
Value of $\pi$ to be used = 3.14.
To Find:
1. Circumference of the outer circle ($C_{outer}$).
2. Circumference of the inner circle ($C_{inner}$).
Solution:
Step 1: Calculate the circumference of the outer circle
The formula for the circumference of a circle is $C \ = \ 2 \pi \times radius$.
For the outer circle, the radius is R = 19 m.
$C_{outer} \ = \ 2 \pi R$
$C_{outer} \ = \ 2 \ \times \ 3.14 \ \times \ 19 \ m$
$C_{outer} \ = \ 6.28 \ \times \ 19 \ m$
$C_{outer} \ = \ 119.32 \ m$
The circumference of the outer circle is 119.32 m.
Step 2: Calculate the radius of the inner circle
The radius of the inner circle (r) is the radius of the outer circle minus the width of the path.
$r \ = \ R \ - \ Width \ of \ path$
$r \ = \ 19 \ m \ - \ 10 \ m$
$r \ = \ 9 \ m$
Step 3: Calculate the circumference of the inner circle
Using the formula $C \ = \ 2 \pi r$ with r = 9 m.
$C_{inner} \ = \ 2 \pi r$
$C_{inner} \ = \ 2 \ \times \ 3.14 \ \times \ 9 \ m$
$C_{inner} \ = \ 6.28 \ \times \ 9 \ m$
$C_{inner} \ = \ 56.52 \ m$
The circumference of the inner circle is 56.52 m.
Final Answer:
Circumference of the outer circle = 119.32 m.
Circumference of the inner circle = 56.52 m.
Question 16. How many times a wheel of radius 28 cm must rotate to go 352 m? $\left(Take \;\pi =\frac{22}{7} \right)$
Answer:
Given:
Radius of the wheel (r) = 28 cm.
Total distance to be covered (D) = 352 m.
Value of $\pi$ to be used = $\frac{22}{7}$.
To Find:
The number of times the wheel must rotate.
Solution:
Step 1: Convert distance to the same unit as the radius
The radius is given in cm, and the distance is given in m. We need to convert the distance to cm.
Since $1 \ m \ = \ 100 \ cm$,
$D \ = \ 352 \ m \ = \ 352 \ \times \ 100 \ cm \ = \ 35200 \ cm$.
Step 2: Calculate the distance covered in one rotation (Circumference)
The distance covered by the wheel in one rotation is equal to its circumference (C).
The formula for circumference is $C \ = \ 2 \pi r$.
Substitute the given values:
$C \ = \ 2 \ \times \ \frac{22}{7} \ \times \ 28 \ cm$
$C \ = \ 2 \ \times \ \frac{22}{\cancel{7}_1} \ \times \ \cancel{28}^4 \ cm$
$C \ = \ 2 \ \times \ 22 \ \times \ 4 \ cm$
$C \ = \ 176 \ cm$
So, the wheel covers 176 cm in one rotation.
Step 3: Calculate the number of rotations
The number of rotations required to cover the total distance is given by:
$Number \ of \ rotations \ = \ \frac{Total \ Distance}{Distance \ per \ rotation}$
$Number \ of \ rotations \ = \ \frac{D}{C}$
$Number \ of \ rotations \ = \ \frac{35200 \ cm}{176 \ cm}$
$Number \ of \ rotations \ = \ 200$
The wheel must rotate 200 times.
Final Answer:
The wheel must rotate 200 times to go 352 m.
Question 17. The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour. (Take π = 3.14)
Answer:
Given:
Length of the minute hand = 15 cm.
Time duration = 1 hour.
Value of $\pi$ to be used = 3.14.
To Find:
The distance the tip of the minute hand moves in 1 hour.
Solution:
In 1 hour (60 minutes), the minute hand of a clock completes one full rotation.
The path traced by the tip of the minute hand is a circle.
The length of the minute hand acts as the radius of this circle.
So, the radius of the circle (r) = Length of the minute hand = 15 cm.
The distance the tip moves in 1 hour is equal to the circumference of the circle traced by it.
The formula for the circumference of a circle is:
$Circumference \ (C) \ = \ 2 \pi r$
Substitute the given values:
$C \ = \ 2 \ \times \ 3.14 \ \times \ 15 \ cm$
$C \ = \ 6.28 \ \times \ 15 \ cm$
$C \ = \ 94.2 \ cm$
Therefore, the tip of the minute hand moves 94.2 cm in 1 hour.
Final Answer:
The tip of the minute hand moves 94.2 cm in 1 hour.
Example 20 to 22 (Before Exercise 11.4)
Example 20. A rectangular park is 45 m long and 30 m wide. A path 2.5 m wide is constructed outside the park. Find the area of the path.

Answer:
Given:
Shape of the park: Rectangle.
Length of the park (inner length, $l_{inner}$) = 45 m.
Width of the park (inner width, $w_{inner}$) = 30 m.
Width of the path constructed outside the park = 2.5 m.
To Find:
The area of the path.
Solution:
The area of the path is the difference between the area of the larger rectangle (park + path) and the area of the inner rectangle (park).
Step 1: Calculate the area of the inner rectangle (park)
$Area_{inner} \ = \ l_{inner} \ \times \ w_{inner}$
$Area_{inner} \ = \ 45 \ m \ \times \ 30 \ m$
$Area_{inner} \ = \ 1350 \ m^2$
Step 2: Calculate the dimensions of the outer rectangle (park + path)
Since the path is 2.5 m wide and constructed outside, we add twice the path width to both the length and the width of the park.
Length of the outer rectangle ($l_{outer}$) = $l_{inner} \ + \ 2 \ \times \ (\text{path width})$
$l_{outer} \ = \ 45 \ m \ + \ 2 \ \times \ 2.5 \ m \ = \ 45 \ m \ + \ 5 \ m \ = \ 50 \ m$
Width of the outer rectangle ($w_{outer}$) = $w_{inner} \ + \ 2 \ \times \ (\text{path width})$
$w_{outer} \ = \ 30 \ m \ + \ 2 \ \times \ 2.5 \ m \ = \ 30 \ m \ + \ 5 \ m \ = \ 35 \ m$
Step 3: Calculate the area of the outer rectangle
$Area_{outer} \ = \ l_{outer} \ \times \ w_{outer}$
$Area_{outer} \ = \ 50 \ m \ \times \ 35 \ m$
$Area_{outer} \ = \ 1750 \ m^2$
Step 4: Calculate the area of the path
Area of the path = Area of the outer rectangle - Area of the inner rectangle
$Area_{path} \ = \ Area_{outer} \ - \ Area_{inner}$
$Area_{path} \ = \ 1750 \ m^2 \ - \ 1350 \ m^2$
$Area_{path} \ = \ 400 \ m^2$
The area of the path is 400 m2.
Final Answer:
The area of the path is 400 m2.
Example 21. A path 5 m wide runs along inside a square park of side 100 m. Find the area of the path. Also find the cost of cementing it at the rate of ₹ 250 per 10 m2.
Answer:
Given:
Shape of the park: Square
Side of the square park (outer side, $s_{outer}$) = 100 m
Width of the path inside the park = 5 m
Rate of cementing =
To Find:
1. Area of the path.
2. Cost of cementing the path.
Solution:
The path runs inside the square park. The area of the path is the difference between the area of the outer square (park) and the area of the inner square (park excluding the path).
Step 1: Calculate the area of the outer square (park)
$Area_{outer} \ = \ (s_{outer})^2$
$Area_{outer} \ = \ (100 \ m)^2 \ = \ 100 \ m \ \times \ 100 \ m \ = \ 10000 \ m^2$
Step 2: Calculate the side length of the inner square
Since the path is 5 m wide inside the park, the side length of the inner square ($s_{inner}$) is obtained by subtracting twice the path width from the outer side length.
$s_{inner} \ = \ s_{outer} \ - \ 2 \ \times \ (\text{path width})$
$s_{inner} \ = \ 100 \ m \ - \ 2 \ \times \ 5 \ m$
$s_{inner} \ = \ 100 \ m \ - \ 10 \ m \ = \ 90 \ m$
Step 3: Calculate the area of the inner square
$Area_{inner} \ = \ (s_{inner})^2$
$Area_{inner} \ = \ (90 \ m)^2 \ = \ 90 \ m \ \times \ 90 \ m \ = \ 8100 \ m^2$
Step 4: Calculate the area of the path
Area of the path = Area of the outer square - Area of the inner square
$Area_{path} \ = \ Area_{outer} \ - \ Area_{inner}$
$Area_{path} \ = \ 10000 \ m^2 \ - \ 8100 \ m^2$
$Area_{path} \ = \ 1900 \ m^2$
The area of the path is 1900 m2.
Step 5: Calculate the cost of cementing the path
The rate is given as
First, find the cost per 1 m2:
Cost per m2 = $\frac{\textsf{₹} 250}{10 \ m^2} \ = \ \textsf{₹} 25 / m^2$
Now, calculate the total cost for the area of the path:
Total Cost = Area of path $\times$ Cost per m2
Total Cost = $1900 \ m^2 \ \times \ \textsf{₹} 25 / m^2$
Total Cost =
Total Cost =
The cost of cementing the path is
Final Answer:
The area of the path is 1900 m2.
The cost of cementing the path is
Example 22. Two cross roads, each of width 5 m, run at right angles through the centre of a rectangular park of length 70 m and breadth 45 m and parallel to its sides. Find the area of the roads. Also find the cost of constructing the roads at the rate of ₹ 105 per m2.
Answer:
Given:
Shape of the park: Rectangle
Length of the park (L) = 70 m
Breadth of the park (B) = 45 m
Number of cross roads = 2
Width of each road (w) = 5 m
Orientation: Roads run at right angles, through the centre, parallel to the sides.
Cost rate of construction =
To Find:
1. Area of the roads.
2. Cost of constructing the roads.
Solution:
Let the road parallel to the length be Road 1 and the road parallel to the breadth be Road 2.
Step 1: Calculate the area of Road 1 (parallel to length)
Length of Road 1 = Length of park = L = 70 m
Width of Road 1 = w = 5 m
$Area_{Road1} \ = \ L \ \times \ w$
$Area_{Road1} \ = \ 70 \ m \ \times \ 5 \ m \ = \ 350 \ m^2$
Step 2: Calculate the area of Road 2 (parallel to breadth)
Length of Road 2 = Breadth of park = B = 45 m
Width of Road 2 = w = 5 m
$Area_{Road2} \ = \ B \ \times \ w$
$Area_{Road2} \ = \ 45 \ m \ \times \ 5 \ m \ = \ 225 \ m^2$
Step 3: Calculate the area of the overlapping region
The two roads intersect at the centre, forming a square region where they overlap.
The side length of this square is equal to the width of the roads.
Side of overlapping square = w = 5 m
$Area_{overlap} \ = \ w \ \times \ w$
$Area_{overlap} \ = \ 5 \ m \ \times \ 5 \ m \ = \ 25 \ m^2$
Step 4: Calculate the total area of the roads
To find the total area covered by the roads, we add the areas of the two roads and subtract the overlapping area (as it was counted twice).
Total Area of Roads = $Area_{Road1} \ + \ Area_{Road2} \ - \ Area_{overlap}$
Total Area = $350 \ m^2 \ + \ 225 \ m^2 \ - \ 25 \ m^2$
Total Area = $575 \ m^2 \ - \ 25 \ m^2$
Total Area = $550 \ m^2$
The total area of the roads is 550 m2.
Step 5: Calculate the cost of constructing the roads
The rate of construction is
Total Cost = Total Area of Roads $\times$ Cost Rate per m2
Total Cost = $550 \ m^2 \ \times \ \textsf{₹} 105 / m^2$
Total Cost =
Total Cost =
The cost of constructing the roads is
Final Answer:
The area of the roads is 550 m2.
The cost of constructing the roads is
Exercise 11.4
Question 1. A garden is 90 m long and 75 m broad. A path 5 m wide is to be built outside and around it. Find the area of the path. Also find the area of the garden in hectare.
Answer:
Given:
Shape of the garden: Rectangle
Length of the garden (inner length, $l_{inner}$) = 90 m
Breadth of the garden (inner breadth, $b_{inner}$) = 75 m
Width of the path = 5 m
Location of the path: Outside and around the garden
To Find:
1. Area of the path.
2. Area of the garden in hectares.
Solution:
Step 1: Calculate the area of the garden (inner rectangle)
The formula for the area of a rectangle is:
$Area \ = \ length \ \times \ breadth$
$Area_{garden} \ = \ l_{inner} \ \times \ b_{inner}$
$Area_{garden} \ = \ 90 \ m \ \times \ 75 \ m$
$Area_{garden} \ = \ 6,750 \ m^2$
Step 2: Calculate the dimensions of the outer rectangle (garden + path)
Since the path is 5 m wide and built outside, we add twice the path width to both the length and the breadth of the garden.
Length of the outer rectangle ($l_{outer}$) = $l_{inner} \ + \ 2 \ \times \ (\text{path width})$
$l_{outer} \ = \ 90 \ m \ + \ 2 \ \times \ 5 \ m \ = \ 90 \ m \ + \ 10 \ m \ = \ 100 \ m$
Breadth of the outer rectangle ($b_{outer}$) = $b_{inner} \ + \ 2 \ \times \ (\text{path width})$
$b_{outer} \ = \ 75 \ m \ + \ 2 \ \times \ 5 \ m \ = \ 75 \ m \ + \ 10 \ m \ = \ 85 \ m$
Step 3: Calculate the area of the outer rectangle
$Area_{outer} \ = \ l_{outer} \ \times \ b_{outer}$
$Area_{outer} \ = \ 100 \ m \ \times \ 85 \ m$
$Area_{outer} \ = \ 8,500 \ m^2$
Step 4: Calculate the area of the path
Area of the path = Area of the outer rectangle - Area of the inner rectangle (garden)
$Area_{path} \ = \ Area_{outer} \ - \ Area_{garden}$
$Area_{path} \ = \ 8,500 \ m^2 \ - \ 6,750 \ m^2$
$Area_{path} \ = \ 1,750 \ m^2$
The area of the path is 1,750 m2.
Step 5: Calculate the area of the garden in hectares
We know that 1 hectare = 10,000 m2.
To convert the area of the garden from m2 to hectares, we divide by 10,000.
$Area_{garden \ in \ hectare} \ = \ \frac{Area_{garden}}{10,000}$
$Area_{garden \ in \ hectare} \ = \ \frac{6,750}{10,000} \ hectares$
$Area_{garden \ in \ hectare} \ = \ 0.675 \ hectares$
The area of the garden is 0.675 hectares.
Final Answer:
The area of the path is 1,750 m2.
The area of the garden is 0.675 hectares.
Question 2. A 3 m wide path runs outside and around a rectangular park of length 125 m and breadth 65 m. Find the area of the path.
Answer:
Given:
Shape of the park: Rectangle
Length of the park (inner length, $l_{inner}$) = 125 m
Breadth of the park (inner breadth, $b_{inner}$) = 65 m
Width of the path = 3 m
Location of the path: Outside and around the park
To Find:
The area of the path.
Solution:
The area of the path is the difference between the area of the outer rectangle (park + path) and the area of the inner rectangle (park).
Step 1: Calculate the area of the inner rectangle (park)
The formula for the area of a rectangle is:
$Area \ = \ length \ \times \ breadth$
$Area_{park} \ = \ l_{inner} \ \times \ b_{inner}$
$Area_{park} \ = \ 125 \ m \ \times \ 65 \ m$
$Area_{park} \ = \ 8,125 \ m^2$
Step 2: Calculate the dimensions of the outer rectangle (park + path)
Since the path is 3 m wide and runs outside, we add twice the path width to both the length and the breadth of the park.
Length of the outer rectangle ($l_{outer}$) = $l_{inner} \ + \ 2 \ \times \ (\text{path width})$
$l_{outer} \ = \ 125 \ m \ + \ 2 \ \times \ 3 \ m \ = \ 125 \ m \ + \ 6 \ m \ = \ 131 \ m$
Breadth of the outer rectangle ($b_{outer}$) = $b_{inner} \ + \ 2 \ \times \ (\text{path width})$
$b_{outer} \ = \ 65 \ m \ + \ 2 \ \times \ 3 \ m \ = \ 65 \ m \ + \ 6 \ m \ = \ 71 \ m$
Step 3: Calculate the area of the outer rectangle
$Area_{outer} \ = \ l_{outer} \ \times \ b_{outer}$
$Area_{outer} \ = \ 131 \ m \ \times \ 71 \ m$
$Area_{outer} \ = \ 9,301 \ m^2$
Step 4: Calculate the area of the path
Area of the path = Area of the outer rectangle - Area of the inner rectangle (park)
$Area_{path} \ = \ Area_{outer} \ - \ Area_{park}$
$Area_{path} \ = \ 9,301 \ m^2 \ - \ 8,125 \ m^2$
$Area_{path} \ = \ 1,176 \ m^2$
The area of the path is 1,176 m2.
Final Answer:
The area of the path is 1,176 m2.
Question 3. A picture is painted on a cardboard 8 cm long and 5 cm wide such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.
Answer:
Given:
Shape of the cardboard: Rectangle
Length of the cardboard (Outer Length, $L_{outer}$) = 8 cm
Width of the cardboard (Outer Width, $W_{outer}$) = 5 cm
Width of the margin along each side = 1.5 cm
To Find:
The total area of the margin.
Solution:
The margin is the area between the outer edge of the cardboard and the inner edge of the painted picture.
Step 1: Calculate the area of the entire cardboard (Outer Area)
The formula for the area of a rectangle is:
$Area \ = \ Length \ \times \ Width$
$Area_{cardboard} \ = \ L_{outer} \ \times \ W_{outer}$
$Area_{cardboard} \ = \ 8 \ cm \ \times \ 5 \ cm$
$Area_{cardboard} \ = \ 40 \ cm^2$
Step 2: Calculate the dimensions of the painted picture (Inner Rectangle)
The margin is 1.5 cm wide on all sides. To find the dimensions of the inner painted area, we subtract twice the margin width from both the length and the width of the cardboard.
Length of the picture (Inner Length, $L_{inner}$) = $L_{outer} \ - \ $$ 2 \ \times \ (\text{margin width})$
$L_{inner} \ = \ 8 \ cm \ - \ 2 \ \times \ 1.5 \ cm \ = \ 8 \ cm \ - \ 3 \ cm \ = \ 5 \ cm$
Width of the picture (Inner Width, $W_{inner}$) = $W_{outer} \ - \ $$ 2 \ \times \ (\text{margin width})$
$W_{inner} \ = \ 5 \ cm \ - \ 2 \ \times \ 1.5 \ cm \ = \ 5 \ cm \ - \ 3 \ cm \ = \ 2 \ cm$
Step 3: Calculate the area of the painted picture (Inner Area)
$Area_{picture} \ = \ L_{inner} \ \times \ W_{inner}$
$Area_{picture} \ = \ 5 \ cm \ \times \ 2 \ cm$
$Area_{picture} \ = \ 10 \ cm^2$
Step 4: Calculate the area of the margin
Area of margin = Area of cardboard - Area of picture
$Area_{margin} \ = \ Area_{cardboard} \ - \ Area_{picture}$
$Area_{margin} \ = \ 40 \ cm^2 \ - \ 10 \ cm^2$
$Area_{margin} \ = \ 30 \ cm^2$
The total area of the margin is 30 cm2.
Final Answer:
The total area of the margin is 30 cm2.
Question 4. A verandah of width 2.25 m is constructed all along outside a room which is 5.5 m long and 4 m wide. Find:
(i) the area of the verandah.
(ii) the cost of cementing the floor of the verandah at the rate of ₹ 200 per m2 .
Answer:
Given:
Dimensions of the room (inner rectangle):
Length ($l_{inner}$) = 5.5 m
Width ($w_{inner}$) = 4 m
Width of the verandah constructed outside = 2.25 m
Rate of cementing =
To Find:
(i) Area of the verandah.
(ii) Cost of cementing the floor of the verandah.
Solution:
The area of the verandah is the difference between the area of the outer rectangle (room + verandah) and the area of the inner rectangle (room).
(i) Finding the area of the verandah
Step 1: Calculate the area of the room (inner rectangle)
$Area_{room} \ = \ l_{inner} \ \times \ w_{inner}$
$Area_{room} \ = \ 5.5 \ m \ \times \ 4 \ m$
$Area_{room} \ = \ 22 \ m^2$
Step 2: Calculate the dimensions of the outer rectangle (room + verandah)
Since the verandah is 2.25 m wide and constructed outside, add twice the verandah width to both the length and the width of the room.
Outer Length ($L_{outer}$) = $l_{inner} \ + \ 2 \ \times \ (\text{verandah width})$
$L_{outer} \ = \ 5.5 \ m \ + \ 2 \ \times \ 2.25 \ m \ = \ 5.5 \ m \ + \ 4.5 \ m \ = \ 10 \ m$
Outer Width ($W_{outer}$) = $w_{inner} \ + \ 2 \ \times \ (\text{verandah width})$
$W_{outer} \ = \ 4 \ m \ + \ 2 \ \times \ 2.25 \ m \ = \ 4 \ m \ + \ 4.5 \ m \ = \ 8.5 \ m$
Step 3: Calculate the area of the outer rectangle
$Area_{outer} \ = \ L_{outer} \ \times \ W_{outer}$
$Area_{outer} \ = \ 10 \ m \ \times \ 8.5 \ m$
$Area_{outer} \ = \ 85 \ m^2$
Step 4: Calculate the area of the verandah
Area of verandah = Area of outer rectangle - Area of inner rectangle (room)
$Area_{verandah} \ = \ Area_{outer} \ - \ Area_{room}$
$Area_{verandah} \ = \ 85 \ m^2 \ - \ 22 \ m^2$
$Area_{verandah} \ = \ 63 \ m^2$
The area of the verandah is 63 m2.
(ii) Finding the cost of cementing the verandah
The cost is calculated by multiplying the area of the verandah by the rate per square meter.
Total Cost = Area of verandah $\times$ Rate of cementing
Total Cost = $63 \ m^2 \ \times \ \textsf{₹} 200 / m^2$
Total Cost =
Total Cost =
The cost of cementing the floor of the verandah is
Final Answer:
(i) The area of the verandah is 63 m2.
(ii) The cost of cementing the verandah floor is
Question 5. A path 1 m wide is built along the border and inside a square garden of side 30 m. Find:
(i) the area of the path
(ii) the cost of planting grass in the remaining portion of the garden at the rate of ₹ 40 per m2 .
Answer:
Given:
Shape of the garden: Square
Side of the square garden (outer side, $s_{outer}$) = 30 m
Width of the path = 1 m
Location of the path: Inside, along the border
Rate of planting grass =
To Find:
(i) Area of the path.
(ii) Cost of planting grass in the remaining portion of the garden.
Solution:
(i) Finding the area of the path
The area of the path is the difference between the area of the outer square (the garden) and the area of the inner square (the garden excluding the path).
Step 1: Calculate the area of the outer square (garden)
$Area_{outer} \ = \ (s_{outer})^2$
$Area_{outer} \ = \ (30 \ m)^2 \ = \ 30 \ m \ \times \ 30 \ m \ = \ 900 \ m^2$
Step 2: Calculate the side length of the inner square (remaining portion)
Since the path is 1 m wide and runs inside the border, the side length of the inner square ($s_{inner}$) is obtained by subtracting twice the path width from the outer side length.
$s_{inner} \ = \ s_{outer} \ - \ 2 \ \times \ (\text{path width})$
$s_{inner} \ = \ 30 \ m \ - \ 2 \ \times \ 1 \ m$
$s_{inner} \ = \ 30 \ m \ - \ 2 \ m \ = \ 28 \ m$
Step 3: Calculate the area of the inner square (remaining portion)
$Area_{inner} \ = \ (s_{inner})^2$
$Area_{inner} \ = \ (28 \ m)^2 \ = \ 28 \ m \ \times \ 28 \ m \ = \ 784 \ m^2$
Step 4: Calculate the area of the path
Area of the path = Area of the outer square - Area of the inner square
$Area_{path} \ = \ Area_{outer} \ - \ Area_{inner}$
$Area_{path} \ = \ 900 \ m^2 \ - \ 784 \ m^2$
$Area_{path} \ = \ 116 \ m^2$
The area of the path is 116 m2.
(ii) Finding the cost of planting grass
Grass is planted in the remaining portion of the garden, which is the inner square.
Area for planting grass = Area of the inner square = 784 m2.
The cost rate is
Total Cost = Area for planting grass $\times$ Cost rate per m2
Total Cost = $784 \ m^2 \ \times \ \textsf{₹} 40 / m^2$
Total Cost =
Total Cost =
The cost of planting grass in the remaining portion of the garden is
Final Answer:
(i) The area of the path is 116 m2.
(ii) The cost of planting grass in the remaining portion is
Question 6. Two cross roads, each of width 10 m, cut at right angles through the centre of a rectangular park of length 700 m and breadth 300 m and parallel to its sides. Find the area of the roads. Also find the area of the park excluding cross roads. Give the answer in hectares.
Answer:
Given:
Shape of the park: Rectangle
Length of the park (L) = 700 m
Breadth of the park (B) = 300 m
Number of cross roads = 2
Width of each road (w) = 10 m
Orientation: Roads run at right angles, through the centre, parallel to the sides.
To Find:
1. Area of the roads (in hectares).
2. Area of the park excluding cross roads (in hectares).
Solution:
Let the road parallel to the length be Road 1 and the road parallel to the breadth be Road 2.
Step 1: Calculate the area of Road 1 (parallel to length)
Length of Road 1 = Length of park = L = 700 m
Width of Road 1 = w = 10 m
$Area_{Road1} \ = \ L \ \times \ w$
$Area_{Road1} \ = \ 700 \ m \ \times \ 10 \ m \ = \ 7,000 \ m^2$
Step 2: Calculate the area of Road 2 (parallel to breadth)
Length of Road 2 = Breadth of park = B = 300 m
Width of Road 2 = w = 10 m
$Area_{Road2} \ = \ B \ \times \ w$
$Area_{Road2} \ = \ 300 \ m \ \times \ 10 \ m \ = \ 3,000 \ m^2$
Step 3: Calculate the area of the overlapping region
The two roads intersect at the centre, forming a square region where they overlap.
The side length of this square is equal to the width of the roads.
Side of overlapping square = w = 10 m
$Area_{overlap} \ = \ w \ \times \ w$
$Area_{overlap} \ = \ 10 \ m \ \times \ 10 \ m \ = \ 100 \ m^2$
Step 4: Calculate the total area of the roads
To find the total area covered by the roads, we add the areas of the two roads and subtract the overlapping area (as it was counted twice).
Total Area of Roads = $Area_{Road1} \ + \ Area_{Road2} \ - \ Area_{overlap}$
$Area_{Roads} \ = \ 7,000 \ m^2 \ + \ 3,000 \ m^2 \ - \ 100 \ m^2$
$Area_{Roads} \ = \ 10,000 \ m^2 \ - \ 100 \ m^2$
$Area_{Roads} \ = \ 9,900 \ m^2$
Step 5: Calculate the total area of the park
$Area_{Park} \ = \ L \ \times \ B$
$Area_{Park} \ = \ 700 \ m \ \times \ 300 \ m$
$Area_{Park} \ = \ 2,10,000 \ m^2$
Step 6: Calculate the area of the park excluding cross roads
Area Excluding Roads = $Area_{Park} \ - \ Area_{Roads}$
Area Excluding Roads = $2,10,000 \ m^2 \ - \ 9,900 \ m^2$
Area Excluding Roads = $2,00,100 \ m^2$
Step 7: Convert the areas to hectares
We know that 1 hectare = 10,000 m2.
Area of Roads in hectares = $\frac{Area_{Roads}}{10,000} \ = \ \frac{9,900}{10,000} \ hectares \ $$ = \ 0.99 \ hectares$.
Area of park excluding roads in hectares = $\frac{Area \ Excluding \ Roads}{10,000} \ $$ = \ \frac{2,00,100}{10,000} \ hectares \ $$ = \ 20.01 \ hectares$.
Final Answer:
The area of the roads is 0.99 hectares.
The area of the park excluding cross roads is 20.01 hectares.
Question 7. Through a rectangular field of length 90 m and breadth 60 m, two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the fields. If the width of each road is 3 m, find
(i) the area covered by the roads.
(ii) the cost of constructing the roads at the rate of ₹ 110 per m2 .
Answer:
Given:
Shape of the field: Rectangle
Length of the field (L) = 90 m
Breadth of the field (B) = 60 m
Number of cross roads = 2
Width of each road (w) = 3 m
Orientation: Roads run parallel to the sides, cut at right angles through the centre.
Cost rate of construction =
To Find:
(i) The area covered by the roads.
(ii) The cost of constructing the roads.
Solution:
Let Road 1 be parallel to the length and Road 2 be parallel to the breadth.
(i) Finding the area covered by the roads
Step 1: Calculate the area of Road 1 (parallel to length)
Length of Road 1 = Length of field = L = 90 m
Width of Road 1 = w = 3 m
$Area_{Road1} \ = \ L \ \times \ w$
$Area_{Road1} \ = \ 90 \ m \ \times \ 3 \ m \ = \ 270 \ m^2$
Step 2: Calculate the area of Road 2 (parallel to breadth)
Length of Road 2 = Breadth of field = B = 60 m
Width of Road 2 = w = 3 m
$Area_{Road2} \ = \ B \ \times \ w$
$Area_{Road2} \ = \ 60 \ m \ \times \ 3 \ m \ = \ 180 \ m^2$
Step 3: Calculate the area of the overlapping region
The roads intersect at the centre, forming a square region.
Side of overlapping square = width of road = w = 3 m
$Area_{overlap} \ = \ w \ \times \ w$
$Area_{overlap} \ = \ 3 \ m \ \times \ 3 \ m \ = \ 9 \ m^2$
Step 4: Calculate the total area covered by the roads
Total Area of Roads = $Area_{Road1} \ + \ Area_{Road2} \ - \ Area_{overlap}$
Total Area = $270 \ m^2 \ + \ 180 \ m^2 \ - \ 9 \ m^2$
Total Area = $450 \ m^2 \ - \ 9 \ m^2$
Total Area = $441 \ m^2$
The total area covered by the roads is 441 m2.
(ii) Finding the cost of constructing the roads
The rate of construction is
Total Cost = Total Area of Roads $\times$ Cost Rate per m2
Total Cost = $441 \ m^2 \ \times \ \textsf{₹} 110 / m^2$
Total Cost =
Total Cost =
The cost of constructing the roads is
Final Answer:
(i) The area covered by the roads is 441 m2.
(ii) The cost of constructing the roads is
Question 8. Pragya wrapped a cord around a circular pipe of radius 4 cm (adjoining figure) and cut off the length required of the cord. Then she wrapped it around a square box of side 4 cm (also shown). Did she have any cord left? (π = 3.14)
Answer:
Given:
Radius of the circular pipe (r) = 4 cm
Side of the square box (s) = 4 cm
Value of $\pi$ to be used = 3.14
To Determine:
Whether Pragya had any cord left after wrapping the square box.
Solution:
First, we need to find the length of the cord Pragya cut. This length is equal to the circumference of the circular pipe.
Step 1: Calculate the circumference of the circular pipe
The formula for circumference is $C \ = \ 2 \pi r$.
Substitute the given values:
$C \ = \ 2 \ \times \ 3.14 \ \times \ 4 \ cm$
$C \ = \ 6.28 \ \times \ 4 \ cm$
$C \ = \ 25.12 \ cm$
So, the length of the cord Pragya cut is 25.12 cm.
Step 2: Calculate the perimeter of the square box
Next, we find the length of cord needed to wrap around the square box. This is equal to the perimeter of the square.
The formula for the perimeter of a square is $P \ = \ 4 \times side$.
$P \ = \ 4 \ \times \ 4 \ cm$
$P \ = \ 16 \ cm$
The length of cord needed for the square box is 16 cm.
Step 3: Compare the length of the cord with the perimeter of the square
Length of the cord = 25.12 cm
Perimeter of the square = 16 cm
Since $25.12 \ cm \ > \ 16 \ cm$, the length of the cord cut is greater than the perimeter of the square box.
Therefore, Pragya did have cord left.
Step 4: Calculate the length of the cord left
Length left = Length of cord - Perimeter of square
Length left = $25.12 \ cm \ - \ 16 \ cm$
Length left = $9.12 \ cm$
Pragya had 9.12 cm of cord left.
Final Answer:
Yes, Pragya had cord left. The length of the leftover cord was 9.12 cm.
Question 9. The adjoining figure represents a rectangular lawn with a circular flower bed in the middle. Find:
(i) the area of the whole land
(ii) the area of the flower bed
(iii) the area of the lawn excluding the area of the flower bed
(iv) the circumference of the flower bed.
Answer:
Given:
Shape of the lawn: Rectangle
Length of the lawn (L) = 10 m
Width of the lawn (W) = 5 m
Shape of the flower bed: Circle
Radius of the flower bed (r) = 2 m
(We will use π = 3.14 for calculations as radius is not a multiple of 7)
To Find:
(i) Area of the whole land (Arealawn).
(ii) Area of the flower bed (Areabed).
(iii) Area of the lawn excluding the flower bed.
(iv) Circumference of the flower bed (Cbed).
Solution:
(i) Area of the whole land (rectangular lawn)
The formula for the area of a rectangle is $Area \ = \ Length \ \times \ Width$.
$Area_{lawn} \ = \ L \ \times \ W$
$Area_{lawn} \ = \ 10 \ m \ \times \ 5 \ m$
$Area_{lawn} \ = \ 50 \ m^2$
The area of the whole land is 50 m2.
(ii) Area of the flower bed (circle)
The formula for the area of a circle is $Area \ = \ \pi r^2$.
$Area_{bed} \ = \ \pi \ \times \ r^2$
$Area_{bed} \ = \ 3.14 \ \times \ (2 \ m)^2$
$Area_{bed} \ = \ 3.14 \ \times \ 4 \ m^2$
$Area_{bed} \ = \ 12.56 \ m^2$
The area of the flower bed is 12.56 m2.
(iii) Area of the lawn excluding the flower bed
This area is the difference between the area of the lawn and the area of the flower bed.
Area excluding bed = $Area_{lawn} \ - \ Area_{bed}$
Area excluding bed = $50 \ m^2 \ - \ 12.56 \ m^2$
Area excluding bed = $37.44 \ m^2$
The area of the lawn excluding the flower bed is 37.44 m2.
(iv) Circumference of the flower bed
The formula for the circumference of a circle is $C \ = \ 2 \pi r$.
$C_{bed} \ = \ 2 \ \times \ \pi \ \times \ r$
$C_{bed} \ = \ 2 \ \times \ 3.14 \ \times \ 2 \ m$
$C_{bed} \ = \ 4 \ \times \ 3.14 \ m$
$C_{bed} \ = \ 12.56 \ m$
The circumference of the flower bed is 12.56 m.
Final Answer:
(i) Area of the whole land = 50 m2
(ii) Area of the flower bed = 12.56 m2
(iii) Area of the lawn excluding the flower bed = 37.44 m2
(iv) Circumference of the flower bed = 12.56 m
Question 10. In the following figures, find the area of the shaded portions:

Answer:
(i) Figure (i)
Given:
Rectangle ABCD with Length AB = 18 cm and Breadth AD = 10 cm.
Point E on AB such that AE = 10 cm.
Point F on AD such that AF = 6 cm.
The unshaded portions are ∆AFE and ∆EBC.
The shaded portion is quadrilateral DECF.
Solution:
First, calculate the area of the whole rectangle ABCD.
$Area_{ABCD} \ = \ Length \ \times \ Breadth \ = \ AB \ \times \ AD$
$Area_{ABCD} \ = \ 18 \ cm \ \times \ 10 \ cm \ = \ 180 \ cm^2$
Next, calculate the dimensions needed for the unshaded triangles:
$EB \ = \ AB \ - \ AE \ = \ 18 \ cm \ - \ 10 \ cm \ = \ 8 \ cm$
$BC \ = \ AD \ = \ 10 \ cm$
Calculate the area of the unshaded triangle AFE:
$Area_{AFE} \ = \ \frac{1}{2} \ \times \ Base \ \times \ Height \ = \ \frac{1}{2} \ \times \ AE \ \times \ AF$
$Area_{AFE} \ = \ \frac{1}{2} \ \times \ 10 \ cm \ \times \ 6 \ cm \ = \ 30 \ cm^2$
Calculate the area of the unshaded triangle EBC:
$Area_{EBC} \ = \ \frac{1}{2} \ \times \ Base \ \times \ Height \ = \ \frac{1}{2} \ \times \ EB \ \times \ BC$
$Area_{EBC} \ = \ \frac{1}{2} \ \times \ 8 \ cm \ \times \ 10 \ cm \ = \ 40 \ cm^2$
The area of the shaded portion is the area of the rectangle minus the areas of the two unshaded triangles.
$Area_{shaded} \ = \ Area_{ABCD} \ - \ Area_{AFE} \ - \ Area_{EBC}$
$Area_{shaded} \ = \ 180 \ cm^2 \ - \ 30 \ cm^2 \ - \ 40 \ cm^2$
$Area_{shaded} \ = \ 180 \ cm^2 \ - \ 70 \ cm^2$
$Area_{shaded} \ = \ 110 \ cm^2$
The area of the shaded portion in Figure (i) is 110 cm2.
(ii) Figure (ii)
Given:
Square PQRS with Side = 20 cm.
Points T on SP and U on SR such that ST = 10 cm and SU = 10 cm.
The unshaded portions are ∆TSU, ∆QRU, and ∆PQT.
The shaded portion is ∆QTU.
Solution:
First, calculate the area of the whole square PQRS.
$Area_{PQRS} \ = \ Side \ \times \ Side$
$Area_{PQRS} \ = \ 20 \ cm \ \times \ 20 \ cm \ = \ 400 \ cm^2$
Next, calculate the dimensions needed for the unshaded triangles:
$PT \ = \ SP \ - \ ST \ = \ 20 \ cm \ - \ 10 \ cm \ = \ 10 \ cm$
$RU \ = \ SR \ - \ SU \ = \ 20 \ cm \ - \ 10 \ cm \ = \ 10 \ cm$
$PQ \ = \ QR \ = \ 20 \ cm$
Calculate the area of the unshaded triangle TSU:
$Area_{TSU} \ = \ \frac{1}{2} \ \times \ Base \ \times \ Height \ = \ \frac{1}{2} \ \times \ SU \ \times \ ST$
$Area_{TSU} \ = \ \frac{1}{2} \ \times \ 10 \ cm \ \times \ 10 \ cm \ = \ 50 \ cm^2$
Calculate the area of the unshaded triangle QRU:
$Area_{QRU} \ = \ \frac{1}{2} \ \times \ Base \ \times \ Height \ = \ \frac{1}{2} \ \times \ QR \ \times \ RU$
$Area_{QRU} \ = \ \frac{1}{2} \ \times \ 20 \ cm \ \times \ 10 \ cm \ = \ 100 \ cm^2$
Calculate the area of the unshaded triangle PQT:
$Area_{PQT} \ = \ \frac{1}{2} \ \times \ Base \ \times \ Height \ = \ \frac{1}{2} \ \times \ PQ \ \times \ PT$
$Area_{PQT} \ = \ \frac{1}{2} \ \times \ 20 \ cm \ \times \ 10 \ cm \ = \ 100 \ cm^2$
The area of the shaded portion (∆QTU) is the area of the square minus the areas of the three unshaded triangles.
$Area_{shaded} \ = \ Area_{PQRS} \ - \ Area_{TSU} \ - \ Area_{QRU} \ - \ Area_{PQT}$
$Area_{shaded} \ = \ 400 \ cm^2 \ - \ 50 \ cm^2 \ - \ 100 \ cm^2 \ - \ 100 \ cm^2$
$Area_{shaded} \ = \ 400 \ cm^2 \ - \ 250 \ cm^2$
$Area_{shaded} \ = \ 150 \ cm^2$
The area of the shaded portion in Figure (ii) is 150 cm2.
Question 11. Find the area of the quadrilateral ABCD.
Here, AC = 22 cm, BM = 3 cm,
DN = 3 cm, and
BM ⊥ AC, DN ⊥ AC
Answer:
Given:
Quadrilateral ABCD.
Diagonal AC = 22 cm.
Height BM (from vertex B to diagonal AC) = 3 cm.
Height DN (from vertex D to diagonal AC) = 3 cm.
To Find:
The area of the quadrilateral ABCD.
Solution:
The diagonal AC divides the quadrilateral ABCD into two triangles: ∆ABC and ∆ADC.
The area of the quadrilateral is the sum of the areas of these two triangles.
Step 1: Calculate the area of ∆ABC
For ∆ABC, the base is AC and the corresponding height is BM.
The formula for the area of a triangle is $Area \ = \ \frac{1}{2} \ \times \ base \ \times \ height$.
$Area_{ABC} \ = \ \frac{1}{2} \ \times \ AC \ \times \ BM$
$Area_{ABC} \ = \ \frac{1}{2} \ \times \ 22 \ cm \ \times \ 3 \ cm$
$Area_{ABC} \ = \ 11 \ cm \ \times \ 3 \ cm$
$Area_{ABC} \ = \ 33 \ cm^2$
Step 2: Calculate the area of ∆ADC
For ∆ADC, the base is AC and the corresponding height is DN.
$Area_{ADC} \ = \ \frac{1}{2} \ \times \ AC \ \times \ DN$
$Area_{ADC} \ = \ \frac{1}{2} \ \times \ 22 \ cm \ \times \ 3 \ cm$
$Area_{ADC} \ = \ 11 \ cm \ \times \ 3 \ cm$
$Area_{ADC} \ = \ 33 \ cm^2$
Step 3: Calculate the area of quadrilateral ABCD
Area of quadrilateral ABCD = Area of ∆ABC + Area of ∆ADC
$Area_{ABCD} \ = \ 33 \ cm^2 \ + \ 33 \ cm^2$
$Area_{ABCD} \ = \ 66 \ cm^2$
Alternate Method:
The area of a quadrilateral can also be calculated using the formula:
$Area \ = \ \frac{1}{2} \ \times \ Diagonal \ \times \ (Sum \ of \ heights \ on \ the \ diagonal)$
$Area_{ABCD} \ = \ \frac{1}{2} \ \times \ AC \ \times \ (BM \ + \ DN)$
$Area_{ABCD} \ = \ \frac{1}{2} \ \times \ 22 \ cm \ \times \ (3 \ cm \ + \ 3 \ cm)$
$Area_{ABCD} \ = \ \frac{1}{2} \ \times \ 22 \ cm \ \times \ 6 \ cm$
$Area_{ABCD} \ = \ 11 \ cm \ \times \ 6 \ cm$
$Area_{ABCD} \ = \ 66 \ cm^2$
Final Answer:
The area of the quadrilateral ABCD is 66 cm2.

